111111111=111+11+1111
の証明が,つぎのようになる:
| 1=1 | (a0)
| | ^11=11 | (a3)
| | ^111=111 | (a3)
| | ^1111=1111 | (a3)
| | ^11111=11111 | (a3)
| | ^111111=111111 | (a3)
| | ^1111111=1111111 | (a3)
| | ^11111111=11111111 | (a3)
| | ^111111111=111111111 | (a3)
| | ^111111111=11111111+1 | (a1)
| | ^111111111=1111111+11 | (a2)
| | ^111111111=111111+111 | (a2)
| | ^111111111=11111+1111 | (a2)
| | ^111111111=1111+1+1111 | (a1)
| | ^111111111=111+11+1111 | (a2)
|
ここで,例えば,証明
1=1^11=11
からの証明
1=1^11=11^111=111
の導出は,つぎの変形による:
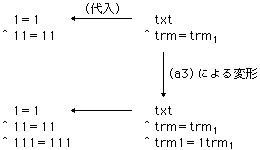
ここで,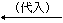 は, は,
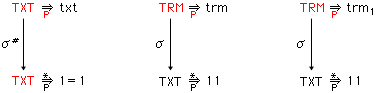
によって定義される代入枠
{(txt,1=1),(trm,11),(trm1,11)}
の下の直接代入
{txt→1=1,trm→11,trm1→11}
である。
|
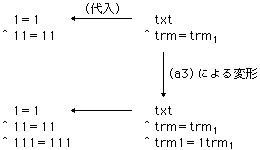
 は,
は,

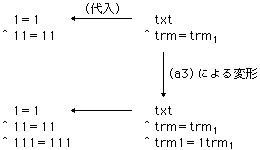
 は,
は,
