"テクスト" を, "一つの言語 L の上のテクスト" として,つぎのように定義する。 即ち,言語 L の上のテクストtとは,有限列を項とする有限列:
この定義では,集合 {αij} を "有限列 {αij|j=1,・・・・,mi} の有限列(i=1,・・・・,n)" と読ませるような形式──分節化してテクストを実現する形式──が想定されている。 各 i=1,・・・・,n に対し,列 {αij|j=1,・・・・,mi} をテクストのtの節と呼ぶ。 "節" の概念は,絵も要素として入り込むということで, "文" (これは絵を含まない)の一般化として導入する。特に,絵を含まない節は文と同じになるとする。 "テクスト" の定義で登場させた "言語" および "絵" の概念については,それぞれ次節とそのつぎの節でこれを規定していくことにする。 2 言語 2.1 言語の定義 われわれは,言語理論の立場から言語を定義する。 この立場からの言語の定義は,可能性として二つである。即ち,文生成のシステムとしての文法をそのまま言語の定義とするか,あるいは,このシステムの現象としての文の集合を言語の定義とするかである。 われわれは,前者をとる。 "文法から生成される文全体の集合" を発想して,これを(文法から生成される)言語と呼ぶことがあるが,われわれはこの立場をとらない((2),§11.2.1)。 2.2 意味論の扱い 言語に関する "シンタクス(統語論)とセマンティクス(意味論)" の発想法があるが,この二分法で言えば,言語理論における言語の記述は,シンタクスの/シンタクスに関わる記述である。 意味論は,言語理論に属さない。(一方,われわれは "言語論" に対しては,意味論を含むものと解釈する。) そもそも,言語自身は意味の契機をもたない。(実際,文としての妥当性 well/ill-formedは,意味とは無関係である(註)。)意味論は言語使用論──言い換えれば,言語の道具化の論──であり,これは実践論である。( "物の意味" が物理科の主題ではなく生活科の主題になるように, "語,文の意味" は,言語理論の主題ではなく実践論の主題になる。) (註) 例えば, "白は黒い。" は文として妥当である。── "非妥当" としてこれに対置されるのは, "は黒い白。" のような記号列。 文として "妥当/非妥当" であるということは,ある状況の中でのそれの使用が "有意味/無意味" であるということとは別のことである。 2.3 "生成文法" 文生成のシステムとしての文法は, "生成文法" として述べることができる。 "生成文法" はチョムスキーのアイデアになるものであるが,チョムスキーの理論──生成変形文法の理論──は,もともと "言語能力" の記述という心理主義的な意識に導かれている。自然言語は,言語能力の実現と見なされる。そこで,言語能力の記述は,現前する自然言語を,そしてそれのみを,完全に生成する規則の記述ということになる。現前する自然言語を説明し尽くすことが,規則の条件である。そして, "生成変形文法理論" という形で,チョムスキーは自ら立てた問題に答えようとしたのであった。 では,この理論によって自然言語に説明がついたかというと,そうはなっていない。しかしこのことは, "生成文法" のアイデアの価値を些かも低めるものではない。 現前している言語を説明することが主題ではなく,一つの言語を現前させることが主題であるとき, "生成文法" のアイデアは有効なのである。 なお, "生成変形文法" の意義は, "文の生成変形" のアイデアにあるのではなく, "文の生成変形" のアイデアを実現するそのスタイルにある。実際, "文の生成変形" の発想は, "生成変形文法" が出る前からある。例えば,論理学における "文形成規則" による文の定義, "公理" による同値な文の規定は, "文生成変形" の発想によっている。 2.4 文法 文法とは,つぎのようなシステム
(1) Vは,二つの有限集合VN,VTの和集合である──即ち,V=VN∪VT かつVN∩VT=∅。 VN の要素は非終端記号(nonterminal symbol)と呼ばれ,VT の要素は終端記号(terminal symbol)と呼ばれる。 ここで,Vの要素の有限列(空な列も含める)全体の集合をV*で表わす。V*の要素を,単に記号列と呼ぶことにする。 (2) Pは記号列の対の有限集合で,その要素は生成規則(production rule)と呼ばれる。 (α,β) ∈ Pを,
(3) SはVN の要素で,初期記号(initial symbol)と呼ばれる。 2.5 記号列の導出 "記号列の導出(derivation)" の概念を,つぎのように定義する: (1) 生成規則α → βと,記号列γ,δに対し,
(2) 記号列αに生成規則の一つを適用して記号列βが生成されるとき, "αは(文法により)直接βを導く" と言う。 またこのことを,
(3) 記号列α1,α2,・・・・,αmにおいて
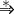 αm αm
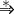 α α
2.6 文 終端記号でなる記号列で,Sから導かれるものを文と呼ぶ。 3 絵 3.1 絵 "絵とは何か?" と問わない限り, "絵" はわれわれにとって自明のものである。本論で, "絵" が主題化されるのは, "言語 L の上のテクスト" を
ここでは, L 上のテクストに現われて,かつ L に外在する記号(要素ないし構成体)一般を, "絵" と呼ぶ。特に, L と異なる言語 L ' の記号で, L 上のテクストに現われたものは,絵である。 絵については, "生成文法" を必須のものとはしない。(必須のものとはしないということであって, "絵の生成文法" を退けるということではない。) "絵の生成文法" の言い回しでここで想定しているのは,つぎのようなことである:
われわれは, "絵に関する生成文法" を全くの観念として述べているのではない。実際,コンピュータ上のCAD(computer assisted design)プログラムがつくる図形データは,生成文法に従っていると見なせる。 さて,絵に関する生成文法が得られているときには, " L の上のテクスト" の定義は, " L および絵生成システム P1, P2,・・・・の上のテクスト" の定義として,つぎのようになる:
3.2 言語記号と絵 L 上のテクストの記号について,それが L の記号であるかそれとも絵であるかは,客観的な事実として決まるのではない。それは,判断されることである。 例えば, L と異なる言語 L ' の記号として最初意識されたもの──このときは,絵──も, L に L ' を埋め込んで考えることができたときには, L の記号になる。 4 論述 ここで,テクストの一つのカテゴリーとして,論述を取り上げることにする。 われわれは, "論述" を "一つの形式化された理論の下の論述" のこととする。したがって,この概念の導入は, "形式化された理論" の概念の導入を伴う。しかも, "形式化された理論" の概念の導入は, "形式的言語" と "論理" の概念の導入を伴うことになる。 4.1 理論 形式化された理論は,一つの形式言語に属する文の(有限)列を生成する系である。理論に対しこのような関係にある言語のことを,われわれは,理論の土台になる言語と呼ぶことにしよう。 文の列の生成は,一定の規則に従う。この規則に従って生成された文の列の各々を,理論の下の論述と呼ぶことにする。 理論の下の論述は,再帰的に定義される。即ち, "論述tから演繹される文 φ をtに追加したものはまた論述である" というように, "論述" は定義される。 "演繹" を,論述の生成規則の遂行のことと定義する。したがってここでは, "演繹" は行為概念である。 理論を規定するものは,土台となる言語,公理,そして推論規則の三つである。われわれは,後の二つを "理論の論理" としてまとめることにしよう。 そこで,理論を規定するとは,言語と論理の二つを特定することである。特に,理論を記述するとは,言語と,論理の二つを記述することである。 言語については既に概念規定したので(§2),残る論理について,以下概念規定を行なう。 4.2 論理 4.2.1 論述,推論規則 "論述" ──理論Tの下の論述──の概念を,文の集合Σに関する "仮定Σの下の論述" として,先ず,つぎの四種類の規則によって定義する:
ここで,(3)i (i=1,2,・・・・,k)はΣに依らないシェマであるとする。これらを理論Tの推論規則と呼ぶ。(論述の定義に先立って推論規則を定義することはできない。) 論述は,仮定として指定された文の集合を核にして,生成される。核が空のとき(即ち,仮定が空集合のとき)には,論述は生じない。 つぎに,ここで定義された "論述" を "狭義の論述" として, "論述" 一般を,狭義の論述の部分列と定義する。 即ち,或る狭義の論述t0 の部分列になるような対象tにも, "論述" の資格があると見なそうというわけである──つぎのように考えることによって:
4.2.2 演繹 文 φ は,仮定Σの下の或る論述に属し得るとき,仮定Σから演繹されると言われる。またこのことを,Σ  φ で表わす φ で表わす
Σに属する任意の文 φ に対し,Σ  φ 。 φ 。
4.2.3 証明 仮定Σの下の論述tと,tの最後に位置する文 φ に対し,tは仮定Σの下での φ の証明であると言う。 したがって,{ φi|i=1,2,・・・・,n} が仮定Σの下での論述であるとき,各k=1,2,・・・・,n に対し,{ φi|i=1,2,・・・・,k} は仮定Σの下での φ k の証明である。 4.2.4 公理 要素が "公理" と呼ばれるところの文の集合Aが指定されているとする。 このとき, "仮定Aの下の論述" を単に "論述" と言い, "仮定Aの下の証明" を単に "証明" と言う。 また,以降,文の集合Σに対するΣ  φ は,公理全体の集合をΑとするときのΣ∪A φ は,公理全体の集合をΑとするときのΣ∪A  φ のことであると約束する。──なおこのとき,文ψに対する{ψ} φ のことであると約束する。──なおこのとき,文ψに対する{ψ}  φ を,ψ φ を,ψ  φ と略記する。また,Σが空集合のときのΣ φ と略記する。また,Σが空集合のときのΣ  φ を, φ を,  φ と書く。 φ と書く。
4.2.5 定理 証明をもつ文を,定理と言う。また,証明をもつことを,証明可能であると言う。 論述は定理の列である(§4.2.3)。そしてこれの逆も成立する(§4.2.1)。特に,一つの定理は,それだけで論述をなす。 公理は定理である。 また,  φ が " φ は定理" の表現になる(註)。 φ が " φ は定理" の表現になる(註)。
(註)  φ は, φ が或る論述に属し得ることを意味する。そしてこれは, φ が証明をもつことと同じ。 φ は, φ が或る論述に属し得ることを意味する。そしてこれは, φ が証明をもつことと同じ。
4.2.6 "推論" われわれは, "推論" を "演繹" と同義の語として導入する。したがってそれは,推論規則にしたがって文を導入する行為を意味する。 推論での文の導入には,推論規則に従う導入と,公理あるいは仮定としての導入( "唐突な導入" )の二つのタイプがあることになる。 5 理論の記述 5.1 言語/理論の記述 言語とは,現前の言語現象に対して,それを生成しているシステムとして想定されるところのものである。言語とは,言わば,言語現象に対する説明のシステムである。 言語の記述は,また一つの言語現象である。よって,これを生成しているシステムとしての言語が新たに想定されることになる。 同様に,理論とは,現前の論述(理論現象として)に対して,それを生成しているシステムとして想定されるところのものである。理論とは,言わば,論述に対する説明のシステムである。 理論の記述は,また一つの論述である。よって,これを生成しているシステムとしての理論が新たに想定されることになる。 5.2 理論の記述の内容 "理論" の定義から,理論Tの記述は,つぎの二つでなる:
理論の使用(応用)についての記述──理論の意味論──は,言語意味論と同様(§2.2),実践論ということにして,ここで言う "理論の記述" には含めない。 5.3 メタ論述,メタ理論,メタ言語 現前の論述を "一つの理論Tの生成する論述t" として解釈し,その生成の仕組みや意義を記述するとしよう。このときひとに "この記述は論理的であるか?" と問われれば,われわれはそうであると答えるだろう。そこでわれわれは,この記述もまた "一つの理論T' の生成する論述t' " であると考えたくなる。 tの記述が或る理論T' の下の一つの論述t' であるということは,t' に現われる各文 φ が,T' を明示する或る論述の下で,T' の定理とされるということである。この意味で,tに関する記述t' は,真なる記述である。 ここで, "メタ論述" , "メタ理論" , "メタ言語" の語を,つぎのように導入する。即ち,論述t' は論述tに対して,理論T' は理論Tに対して,そしてT' の土台になっている言語はTの土台になっている言語に対して,それぞれメタであると言う。 理論Tの記述は,tが空な論述の場合のtの記述と見なせる。 非明示的な理論T' を明示する論述を,或る理論T″の下の論述と考えるとき,T″は非明示的である。この意味で,われわれは "非明示的な理論" から免れることはできない。 5.4 記号と絵 理論Tを記述する論述t' を理論T' の下の論述と考えるとき,Tの記号や文がt' の中に現われているという事態は,どのように解釈されるべきか。 二通りの解釈が可能である。一つは,《t' の中に現われているTの記号および文は,T' の記号および文でもある》とするものである。特に,T' の土台となる言語はTの土台となる言語を含む,のような解釈。 もう一つは,《t' の中で,Tの記号や文は "絵" である》とするものである。このときt' は,T' の記号,文としての "ことば" と,Tの記号,文としての "絵" と,その他の絵と,そして個々のことばや絵を画定する記号(例えば,空白)で構成されている。 この二つのどちらの解釈においても,t' に現われているTの記号,文がT' の或る記号,文に同じであるときには,それが正しくTの記号,文として読まれることが必要になる。特にそのために,Tの記号,文であることを明示する方法が導入されたりする。普通よく用いられている方法は,前後に "," (引用符)をつけるとか,特殊字体にするとかである。 6 "自己言及" 6.1 メタ理論の無際限性 "論述に言及する論述" の現象は, "メタ理論" の概念で解釈される。そしてこの場合,任意の理論Tに対し,
例えば,形式的自然数論Tの文 " ¬ (0 → 0)" から始めて,
→ " " " ¬ (0 ∈ 0)"は文。"は文。" → " " " " ¬ (0 ∈ 0)"は文。"は文。"は文。" → ・・・・ のような "言及の無限列" を考えることができる。最初の (1) " " ¬ (0 ∈ 0)"は文。" は, (1)' " " ¬ (0 ∈ 0)"はTの文。" として,形式的自然数論Tを対象化するものになる。 つぎの (2) " " " ¬ (0 ∈ 0)"は文。"は文。" は, (2)' " " " ¬ (0 ∈ 0)"はTの文。"はT1の文。" として, "Tのメタ理論T1" を対象化するものになる。実際,端的に, " " " ¬ (0 ∈ 0)"はTの文。" は,Tの記号列ではない。但し,
実際,つぎの (3) " " " " ¬ (0 ∈ 0)"は文。"は文。"は文。" は, (3)' " " " " ¬ (0 ∈ 0)"はTの文。"はT1の文。"はT2の文。" として, "T1のメタ理論T2" を対象化するものになる。何故なら,
で言及されるT1は,T1 の対象ではないから》 以下同様に,理論T3,T4,・・・・が意識対象化される。 6.2 普遍言語 "論述に言及する論述" を発想するとき,任意の理論Tに対し,列:
例えば,§6.1の
→ " " " ¬ (0 ∈ 0)"はTの文。"はT1の文。" → " " " " ¬ (0 ∈ 0)"はTの文。"はT1の文。"はT2の文。" → ・・・・ では,T1の土台となる言語 L1 として,これらの言及が全て L 1 の文になるようなもの(言い換えると, "は文。" を追加する操作が L1 の中で閉じるようなもの)をとることは,可能である──実際,例えば自然言語。 われわれは,つぎのような予想をもつ:
6.3 対象と記号 《一つの言語の上での, "論述に言及する論述" の無際限の繰り返し,およびメタ理論の無際限の現出》が発想可能なのは, "論述の対象" と "言語の記号" が異なる概念だからである。 二つの理論T,T1の土台となる言語が同じ── L とする──で, L の或る記号が理論T1において "理論T" の意味で使われるということは,何ら特別なことではない。肝心な点は,Tにおいては, L の或る記号を "理論T" の意味で使うことはあり得ない,ということである。 6.4 自己言及の不可能 "理論Tの中でのT自身への言及は,可能か否か?" いま,この問いが論理的な判断を要求するものとして発せられているとしよう。 論理的に判断しようとするとき,判断が従うべき論理が要る。 論理は,一つの理論の論理のことである。したがって,理論Tの中でのT自身への言及が可能か否かは,一つの理論の下で判断される。 しかし,《理論Tの中でのT自身への言及は可能》を結論する理論がつくれたとして,これによって,われわれは《理論Tの中でのT自身への言及は可能》と考えるようになるであろうか。 いま,《箱の中に居て箱を見ることは,可能か否か?》の問いに論理的に答えることが,問題になったとしよう。そして,《箱の中に居て箱を見ることは可能》を結論する理論を作為できたとしよう。このとき,われわれはどのように考えるか。 われわれは,その理論で言う "箱" はわれわれが了解している "箱" のことではない,というように考えるであろう。 われわれは,《箱の中に居て箱を見ることは可能》を結論する理論を許さない。箱の中に居て箱を見ることが不可能であることを知っており,しかも,理論によって知っているわけではないからである。 全く同じ意味で,われわれは,《理論Tの中でのT自身への言及は可能》を結論する理論を端的に許さない。そのような理論に対しては,その理論で言う "理論" はわれわれが了解している "理論" のことではない,という処し方をする。《理論Tの中でのT自身への言及が不可能》であることを知っており,しかも,理論によってこのことを知っているわけではないからである。 6.5 "自己言及" の集合的解釈── "自分自身を元とする集合" 文を, "対象xへの言及" ──言い換えると, "対象xに述語づけるもの" ──として,捉えるとしよう。そして,理論Tの中で言及可能な対象xの総体を,Uと定義する。 "Tの中でのT自身への言及" は, "Tの中でのUへの言及" と解釈される。そしてこのとき,Tの中でT自身に言及できるということは,U ∈ Uと同じことになる。 "Tの中でのT自身への言及" を集合で解釈しようとして,集合Uが導入された。しかしわれわれは,Uの導入があくまでも見掛けのものであることに,注意しなければならない。即ち, "理論Tの中で言及可能な対象xの総体" を対象化することの妥当性が,疑われなければならないのである。 "自己言及" は,虚偽の概念である。したがって,これの定式化はもともとあり得ない。集合Uの導入による先の定式化は,見せかけの定式化なのである。虚偽は,Uの定義のところにある。Uの定義は,見せかけである。 6.6 "自分自身を元とする集合" の禁止 われわれは, "自分自身を元とする集合" の概念を,端的に禁じている。 "自分自身を元とする集合" が虚偽であることを,理論によって了解しているのではない。 われわれは,了解に至るためではなく,既に了解していることを合理化するために,理論を用いる。即ち, "自分自身を元とする集合" を禁じるために,理論を導入する。 例えば,Zermelo-Fraenkel の集合論はこのようなものになっている(註)。 (註) a ∈ aは,
 ¬ (a ∈ a)。 ¬ (a ∈ a)。
6.7 "自己言及のパラドクス" "自己言及のパラドクス" という言い回しに出会うことがあるが,《 "自己言及のパラドクス" をつくることはできない》の意味で, "自己言及のパラドクス" はあり得ない。 実際われわれは, "理論Tの中でのT自身への言及" の概念からパラドクスを導けない。 "自分自身を元とする集合" の概念からパラドクスを導けない。 また, "自己言及することば" のパラドクスも,
例1. "ここで述べていることは正しい" では,〈ここで述べていること〉は "ここで述べていることは正しい" 自身ではなく,これの他にあることになる。 例2. "どんな言葉でも表現できないことがら" では, "どんな言葉でも表現できないことがら" 自身は, "どんな言葉でも" から除外される。 6.8 "ラッセルのパラドクス" "ラッセルのパラドクス" が,自己言及のパラドクスのように紹介されることがあるが,これは正しくない。 ラッセルのパラドクス" とは,つぎのようなパラドクスである:
Nが正規ならば,Nの定義( "すべての正規集合の集合" )から,Nは自分自身を元とする。 "正規" の定義から,Nは非正規。また,Nが非正規ならば, "正規" の定義から,Nは自分自身を元として含む。そしてNの要素であるN自身は,Nの定義から,正規集合。 しかしこのパラドクスは, "理論Tの中でのT自身への言及" ないし "自分自身を元とする集合" の概念に起因しているのではない。 "すべての正規集合の集合" ──特に, "すべて" ──の概念に起因しているのである。 7 理論の形式化 7.1 非形式的理論 われわれはここで, "非形式的理論" の概念を導入する(註)。 非形式的理論は,論述生成の規則が明示的に特定されていない,論述生成のシステムである。ここで "論述" の条件は,その中の各文が "真" であり,文の逐次的導出が "論理的" であるということが,われわれに了解される,ということである。 われわれのこの "了解" は, "直観的" と言いたくなるようなものもあるが,一般にはそうではない。やはり "計算" を経て了解に至る。しかしここでは, "計算" に根拠を与える原初的な規則の明示がない限り "計算" は明示できない,という立場をとるのである。したがって,非形式的理論の論述を論述として成立させているものは,《われわれの了解が何故か奇妙にも一致する》という事実,ということになる。 われわれが実践的に出会う理論は,非形式的理論である。それは霧の中から姿を現わしている風情のものである。そこには,霧の内と外の区切りが存在しない。 この比喩では,計算規則をより根源的な規則へと還元することが,霧を後退させることに当たる。そして,理論の形式化が,霧を完全に晴らすことに当たる。 (註) ここでの "非形式的理論" の定義は,同時に, "形式的" を非日常語的に定義するものである。 "形式的" の日常語的意味で言えば,理論はすべて形式的である。実際,人間に関わるもので形式的でないものはない。また, "形式化をさらに進める" という言い回しにわれわれが不合理を感じないように,日常語では, "形式的" とは,あくまでも相対的な概念である。 また,日常語の "形式化" には, "意味の捨象" の意味もある。しかし,本節で主題化する "理論の形式化" に, "意味" の問題は入ってこない。 7.2 理論の形式化 理論の形式化の主題では,形式化される非形式的理論Tとこれの形式化になる形式的理論  を明示的に登場させることになる。 を明示的に登場させることになる。
Tと  の明示ないしTの の明示ないしTの  への形式化は,非明示的な或る理論T' の下の一論述の実現として実践される(註)。特に,T' はTと への形式化は,非明示的な或る理論T' の下の一論述の実現として実践される(註)。特に,T' はTと  の両方を記述できる理論である。 の両方を記述できる理論である。
(註) T' が非明示的であるとは,T' の明示が不可能だということではない。《T' の明示は,また,別の或る一つの非明示的な理論の一論述の実現として実践される;この意味で,われわれは "非明示的な理論" から免れることはできない》ということである。 7.3 形式化の内容 T' の下で,Tの文の  の文による表現がつくられる。 の文による表現がつくられる。
T' の記号の中には,特に,  , , 
 は, T の文 φ と は, T の文 φ と  φ のように結合し, " φ はTで真" を意味する(註)。 φ のように結合し, " φ はTで真" を意味する(註)。
 は, は,  の文 の文 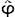 と と  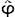 のように結合し, " のように結合し, " 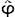 は は  の定理" (§4.2.5)を意味する。 の定理" (§4.2.5)を意味する。
そして,Tの文 φ が  の文 の文 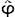 によって表現されるということが, によって表現されるということが,
(*) (T' において)  φ と φ と  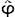 は同値 は同値
が成立する──言い換えると,(*)がT' の論述を形成する文になる──ことと定義される。(詳しくは,§10 参照。) (註) 記号  を,ここでは記号 を,ここでは記号  と区別するためだけに用いる。記号 と区別するためだけに用いる。記号  のこのような使用は,通常のもの ((2), §12.9.3) ではない。 のこのような使用は,通常のもの ((2), §12.9.3) ではない。
8 論理学の主題になる "論理" 8.1 理論のシェマ 複数の理論が対象化されると,そこに "理論のシェマ" の主題が立つようになる。 "シェマ" は,以下のもののセットとして考えられる:
(1-2) 文生成規則
(2-2) 特定の推論規則 理論のシェマの概念が持たれるとき,理論の特定が,
8.2 シェマ 理論のシェマとして対象化される文生成規則,公理,推論規則では,公理はシェマに,生成規則,推論規則はシェマに関する規則に,それぞれ代えられている。 理論Tのシェマは,Tのメタ理論の対象である。TのシェマはTのメタ理論の下で見出され,記述される。 Tのメタ理論T' におけるTのシェマの記述は,《Tの記号列をT' の変項記号に換える》という仕方で行なわれる。 例えば,a,b,cがTの定項記号のすべてであって,Tの記号*に対する三つの記号列:
φ * φ (ここで φ は,T' における変項記号)のようにシェマとして表現することで対象化する。 8.3 理論の記述におけるシェマの使用 理論Tの公理がシェマの形で記述され,文形成規則,推論規則がシェマに関する規則の形で記述されることは,特殊なことでなく,普通のことである。シェマの使用に対しては記述の省力化の解釈も立つが,それがシェマの形で記述する第一の理由になるのではない。 多くの場合,一つのシェマの内容になる記号列が無限個あり,列挙不可能であるという理由から,シェマによる表現が必須になるのである。 8.4 論理学の主題になる "論理" "理論のシェマ" の概念は,論理学で "各種論理" と言うときの "論理" と一致する。 論理学において各種論理の "文生成規則" , "公理, "推論規則" として述べられているものは,正しくは,文生成規則,公理,推論規則ではない。これらは必ずシェマを含むが,そのシェマには内容がないからである。──シェマを埋めるべき言語をはじめから用意しないわけであるから,当然このようになる。 そこで逆に,これらのシェマに内容を与えることが,理論の実現ということになる。勿論,論理学で "各種論理" と言うときの "論理" (例えば,命題論理,述語論理)は,理論ではない。 8.5 例(1)── "命題論理" "命題論理" は,以下に示す記号(特定の記号と記号シェマ),文形成規則(シェマに関する規則として),公理(シェマとして),推論規則(シェマに関する規則として)のセットである。これを部分にもつ理論を,命題論理を伴う理論と呼ぶことにする。 8.5.1 記号 "命題論理" を定義する記号(終端記号)──簡単に, "命題論理の記号" ──には,つぎの二種類がある:
(2) 論理記号(logical symbol) 非論理記号は,つぎのものである:
(1-2) 変項記号(文変項記号) 非論理記号を特定せずに "非論理記号の存在" を条件と定めるこの定義において, "非論理記号" は記号シェマとして導入されていることになる。 論理記号は,つぎのものである:
∧ , ¬ (註2) (2-2) 括弧: ( , ) (註1) " ¬ " に見るように,ここでの "connection" には,既に, "文と文を結びつける" という意味はない。 (註2) ∧ は連言(conjunction)と呼ばれ,日常語の "and"を想定している。 ¬ は否定(negation)と呼ばれ,日常語の "not" を想定している。 8.5.2 文形成規則 "命題論理" を定義する文形成規則──簡単に, "命題論理の文形成規則" ──は,式形成規則と文の定義の二段階で述べられる。 式は,つぎのように再帰的に定義される:
(2) 定項記号は式である; (3) 式 φ に対し( ¬ φ) は式; (4) 式 φ ,ψに対し,( φ ∧ ψ)は式; (5) 上の(1)から(4)の適用で生成されるもののみが,式である. そして,変項記号を含まない式を,文と定義する。 8.5.3 公理 "命題論理" を定義する公理──簡単に, "命題論理の公理" ──は,つぎのものである(註):
(A2) ( φ → (ψ → θ)) → (( φ → ψ) → ( φ → θ)) (A3) ( ¬ ψ → ¬ φ) → ( φ → ψ) (註) 簡略記号として,
→ :含意(implication; "implies"), ↔ :同値(equivalence; "if and only if")
(2) (( ¬ φ) ∨ ψ) を ( φ → ψ) と略記する; (3) (( φ → ψ) ∧ (ψ → φ)) を ( φ ↔ ψ) と略記する. 8.5.4 推論規則 "命題論理" を定義する推論規則──簡単に, "命題論理の推論規則" ──は,分離規則(rule of detachment,あるいは Modus Ponens)と呼ばれるつぎのものである:
8.6 例(2)──述語論理 "述語論理" は,以下に示す記号(特定の記号と記号シェマ),文形成規則(シェマに関する規則として),公理(シェマとして),推論規則(シェマに関する規則として)のセットである。これを部分にもつ理論を,述語論理を伴う理論と呼ぶことにする。 8.6.1 記号 "述語論理" を定義する記号(終端記号)──簡単に, "述語論理の記号" ──には,つぎの二種類がある:
(2) 論理記号(logical symbol) 8.6.1.1 非論理記号 非論理記号にはつぎの三種類がある:
(2) 関数記号 (3) 定項記号(constant symbol) (註2) 関係記号および関数記号のそれぞれに対し,一つの自然数nが対応している。nが対応している関係記号および関数記号は,それぞれn項(n-arguments)関係記号,n変数(n-arguments)関数記号と呼ばれる。 非論理記号を特定せずに "非論理記号の存在" を条件と定めるこの定義において, "非論理記号" は記号シェマとして導入されていることになる。 (註1) あるいは "述語定項(predicate constant)" 。 (註2) あるいは, "個体定項(individual constant)" とも呼ばれる。 8.6.1.2 論理記号 論理記号には,つぎのものがある:
(註1) あるいは,( "個体定項" に対して) "個体変項" とも呼ばれる。 (註2) あるいは "量化子" とも言う。
[廣瀬健,横田一正,『ゲーデルの世界』,海鳴社,1985,p.70] (註3) 全称限量子(universal quantifier "for all") 8.6.2 文形成規則 "述語論理" を定義する文形成規則──簡単に, "述語論理の文形成規則" ──は,項形成規則,式形成規則,文の定義の三段階で述べられる。 8.6.2.1 項 項は,つぎのように再帰的に定義される:
(2) 定項記号は項である; (3) Fがn項関数記号で,t1,・・・・,tnが項であるとき,記号列F(t1・・・・tn)も項である; (4) 上の(1)から(3)の適用で生成されるもののみが,項である. 8.6.2.2 式 式の定義では,先ず原子式(atomic formula)がつぎのように定義される:
(2) n項関係記号Rと項t1,・・・・,tnに対し,記号列R(t1・・・・tn)は原子式. そして式(註)をつぎのように再帰的に定義する:
(2) 式 φ ,ψに対し,( φ ∧ ψ),( ¬ φ) は式; (3) 変項vと式 φ に対し,( ∀ v) φ は式; (4) 上の(1)から(3)の適用で生成されるもののみが,式である. ここで,簡約記号 ∨ , → , ↔ を命題論理のときと同様に導入し,さらに,( ∃ v) φ を ¬ (( ∀ v)( ¬ φ)) のこととして,記号 ∃ ( "存在限量子existential quantifier" )を導入する。 (註) "論理式" とも呼ぶ。 8.6.2.3 自由変項,束縛変項 式の中の変項記号xに対し,xに〈作用〉する限量子があるとき,xは〈束縛〉されていると言い,そうでないとき,〈自由〉であると言う。 8.6.2.4文 最後に,文(註)を,自由変項を含まない式と定義する。 各モデルについてそれの真偽が無条件に定まる式を "文" と定義しようとして,このような定義になる。実際,自由変項を含む式は,自由変項に何が代入されるかによって真偽が定まるのであって,無条件には,真偽が定まらない。 なお以降,つぎの記号法を用いる:
(註) "閉論理式" とも呼ぶ。所謂 "開放文" は,自由変項を含む式のことであり,ここで言う "文" ではない。 8.6.3 公理 "述語論理" を定義する公理──簡単に, "述語論理の公理" ──は,論理公理(logical axiom)としてつぎの2つのグループに分けられる:
(2) 限量子公理(quantifier axiom); つぎのように定義される論理公理が,文公理である:
また,つぎのように定義される論理公理が,限量子公理である:
(2) φ ,ψを式,vを変項記号,tを項とする。 φ において自由なvをtで置換することによってψが得られ,かつこのtの置換においてtのどの変項も自由であるとき,
(註) vが φ において自由であることを φ(v) で表わし, φ のvをtに置換してえられる式を φ(t) で表わせば,( ∀ v) φ → ψは ( ∀ v) φ(v) → φ(t) で表わされる。 8.6.4 推論規則 "述語論理" を定義する推論規則──簡単に, "述語論理の推論規則" ──は,つぎの二つである:
(2) 一般化規則(rule of generalization):
8.6.5 命題論理との関係 述語論理は,命題論理を部分に持つ。 9 理論の例──形式的自然数論 9.1 自然数論の論述 形式的自然数論  は,ある一定の論述を生成するシステムである。そして,この は,ある一定の論述を生成するシステムである。そして,この  を対象化して示す論述は, を対象化して示す論述は,  とは別の或る理論T' が生成するところのものである。 とは別の或る理論T' が生成するところのものである。
T' は,非形式的自然数論を含んでいる。 9.2 階数 形式的自然数論  を記述する理論T' は,対象に関する階数(型)の概念を導入する。階数とは,つぎのように定義される概念である。 を記述する理論T' は,対象に関する階数(型)の概念を導入する。階数とは,つぎのように定義される概念である。
即ち,個々の自然数を,基礎となる対象の意味で1階の対象(object of type 1)とし,そして,n階の対象のみを元とする集合の各々を,n+1階の対象とする。 一般に,階数によって分類されているところの自然数ないし自然数から導かれる集合を対象とする理論は,型の理論(theory of type)と呼ばれる。自然数論は,型の理論の一つである。 9.3 土台となる言語 形式的自然数論  は,以下のように定義される言語 L を土台とする。 は,以下のように定義される言語 L を土台とする。
9.3.1 記号 L の記号(終端記号)は,つぎの二種類である:
(2) 論理記号(logical symbol) 9.3.1.1 非論理記号 非論理記号にはつぎのものがある:
(2) 1変数関数記号: ' (3) 定項記号 : 0 9.3.1.2 論理記号 論理記号には,つぎのものがある:
(註) 記号ξ(1,1)は,これひとまとまりで一つの記号である。ξ, (, 1, ,, 1, ) のように分析されるものではない。ξ(1,2) 以下についても同様。 "1階の変項記号:ξ(1,1),ξ(1,2),ξ(1,3),・・・・・" は,(形式的自然数論  を論述する)理論T' の文である。そしてT' において,われわれは記号:ξ(1,1),ξ(1,2),ξ(1,3),・・・・・における 1,2,3,・・・・を自然数として把捉できる。しかし, を論述する)理論T' の文である。そしてT' において,われわれは記号:ξ(1,1),ξ(1,2),ξ(1,3),・・・・・における 1,2,3,・・・・を自然数として把捉できる。しかし,  において 1,2,3,・・・・ は分析されない。 において 1,2,3,・・・・ は分析されない。
9.3.2 文形成規則 文形成規則は,項形成規則と式形成規則をそれの要素とする。 9.3.2.1 項 1階の項が,つぎのように再帰的に定義される:
(2) 1階の変項記号は1階の項である; (3) 1階の項tに対し,t' も1階の項である(註); (4) 上の(1)から(3)の適用で生成されるもののみが,1階の項である. そして,n=2,3,・・・・ について,n階の項がn階の変項記号のこととして定義される。 したがって,つぎの形の項が閉項(変項記号を含まない項)の全てである,
(註) この言い回しの中のtは,理論T' の変項記号である。そして, "1階の項tに対し,t' も1階の項である" は,本来つぎのように言うべきところを簡略化して言ったものである:
 の記号列で1階の項であるものの右端に記号 ' を加えて得られる の記号列で1階の項であるものの右端に記号 ' を加えて得られる  の記号列は,再び1階の項である" の記号列は,再び1階の項である"
9.3.2.2 式 式の定義では,先ず原子式(atomic formula)がつぎのように定義される:
そして式を,述語論理の場合と同様,つぎのように再帰的に定義する:
(2) 式 φ ,ψに対し,( φ ∧ ψ),( ¬ φ) は式; (3) 変項vと式 φ に対し,( ∀ v) φ は式; (4) 上の(1)から(3)の適用で生成されるもののみが,式である. ここで,簡約記号 ∨ , → , ↔ , ∃ を,述語論理のときと同様に導入する。 さらに,n階の項s,tに対し,
(註1) この言い回しの中のs,tは,理論T' の変項記号である。そして, "n階の項sとn+1階の項tに対し,s ∈ tは原子式" は,本来つぎのように言うべきところを簡略化して言ったものである: "  の記号列でn階の項であるものと, の記号列でn階の項であるものと, の記号 ∈ と,そしてTの記号列でn+1階の項であるものをこの順につなげるとき,得られる の記号 ∈ と,そしてTの記号列でn+1階の項であるものをこの順につなげるとき,得られる  の記号列は原子式" の記号列は原子式"
これに類する簡略表現は以下頻繁に登場するが,今後は一々断らない。 (註2) この言い回しは,つぎの言い回しの簡略化である:
 の記号列‘( ∀ ξ(n+1,1))(’と,n階の項である の記号列‘( ∀ ξ(n+1,1))(’と,n階の項である  の記号列(sと名付ける)と, の記号列(sと名付ける)と, の記号列‘ ∈ ξ(n+1,1)→’と,n階の項である の記号列‘ ∈ ξ(n+1,1)→’と,n階の項である の記号列(tと名付ける)と,そして の記号列(tと名付ける)と,そして の記号列
‘ ∈ ξ(n+1,1))’
をこの順につなげて得られるTの記号列を,sと名付けた記号列と,記号=と,そしてtと名付けた記号列をこの順につなげて得られる記号列で,表現する" の記号列
‘ ∈ ξ(n+1,1))’
をこの順につなげて得られるTの記号列を,sと名付けた記号列と,記号=と,そしてtと名付けた記号列をこの順につなげて得られる記号列で,表現する"
9.3.2.3文 式の中の変項記号xに関する〈束縛〉,〈自由〉の概念を,述語論理の場合と同様に定義する。そして最後に,文を,自由変項を含まない式と定義する。 9.4 論理 自然数論の論理は,以下に示す公理と推論規則の系である。 9.4.1 公理 自然数論の公理は,つぎの四種類である:
(2) 述語論理の公理(§8.6.3); (3) 内包の公理; (4) 外延性の公理. 自然数の公理は,以下のものである → 1):
2°ξ(1,1)' =ξ(1,2)' →ξ(1,1)=ξ(1,2) 3°(0 ∈ ξ(2,1) ∧ ( ∀ ξ(1,1)) (ξ(1,1) ∈ ξ(2,1) → ξ(1,1)' ∈ ξ(2,1))) →( ∀ ξ(1,1)) (ξ(1,1) ∈ ξ(2,1)) 内包の公理(axiom of comprehension)とは,n階の変項x,n+1階の変項y,そしてyを自由変項としてふくまない式 φ に対する,つぎの式である (註2):
外延性の公理(axiom of extenshionality)とは,つぎの式である (註3):
(ξ(n,1) ∈ ξ(n+1,1) ↔ ξ(n,1) ∈ ξ(n+1,2)) →ξ(n+1,1)=ξ(n+1,2) (註1) これは, "ペアノの公理" である。なお,変項記号については,§9.3.1.2 を参照のこと。 (註2) "yを外延とするx一般(概念)の内包が φ , φ を内包とするx一般(概念)の外延がy。" (註3) "n+1階の対象は,その元となるn階の対象の全体によって確定する。" 9.4.2 推論規則 形式的自然数論  の推論規則は,述語論理の推論規則──分離規則と一般化規則──(§8.6.4)である。 の推論規則は,述語論理の推論規則──分離規則と一般化規則──(§8.6.4)である。
9.5 命題論理,述語論理の随伴 形式的自然数論  は,述語論理を伴う理論であり,特に,命題論理を伴う理論である。 は,述語論理を伴う理論であり,特に,命題論理を伴う理論である。
9.6 自然数論の一意性 形式的自然数論は,同型を許して一意である。 9.7 加法と乗法 9.7.1 関数の帰納的定義 n≧1とする。自然数xにn階の対象を対応させる関数──理論T' における関数── φ (x)の定義で,つぎの形式にしたがうものを,帰納的定義(recursive definition)と言う。即ち,自然数xとn階の対象ηにn階の対象を対応させる関数f(x,η)(註)と,n階の対象tに対し,
φ (x' )=f(x, φ (x)) このとき,
φ (1)= φ (0' )=f(0, φ (0))=f(0,t) φ (2)= φ (1' )=f(1, φ (1))=f(1,f(0,t)) ・・・・ (註) x,ηはT' の変項記号で,f(x,η)はつぎのような記号列:
(2) f(x,η)の中のxとηを,それぞれ自然数である  の記号列とn階の対象である の記号列とn階の対象である  の記号列で置換して得られる の記号列で置換して得られる  の記号列は,n階の対象。 の記号列は,n階の対象。
そしてfは,自然数である  の記号列とn階の対象である の記号列とn階の対象である  の記号列の対(つい)に対し,f(x,η)の中のxとηを,それぞれこの対の前項と後項で置換して得られる の記号列の対(つい)に対し,f(x,η)の中のxとηを,それぞれこの対の前項と後項で置換して得られる  の記号列(n階の対象)を対応させる関数。 の記号列(n階の対象)を対応させる関数。
9.7.2 加法と乗法 前節の φ の定義で,n=1とし,f(x,η)としてη' をとる (註1):
φ (x' )= φ (x)' そして,自然数xに対する自然数 φ (x)を,
このとき, φ の定義がつぎのように書き換えられる:
t+x' =(t+x)' 同様に,t × xをつぎのように定義する:
t × x' =t × x+t
(a+b)+c=a+ (b+c) a × b=b × a (a × b) × c=a × (b × c) (a+b) × c=a × c+b × c (註1) x,ηはT' の変項記号で,f(x,η)は記号列η' 。そしてfは,自然数(1階の対象)の対(つい)に対し,記号列f(x,η)──即ち,記号列η' ──の中のηを,この対の後項で置換して得られる自然数を対応させる関数。 (註2) 即ち,自然数である  の記号列(xと名付ける)に対する φ の値──自然数である の記号列(xと名付ける)に対する φ の値──自然数である  の記号列──を,記号列tと,記号+と,記号列xをこの順につなげて得られる記号列で表わす。 の記号列──を,記号列tと,記号+と,記号列xをこの順につなげて得られる記号列で表わす。
9.8 順序関係 自然数a,bに対し,
このとき,以下が(シェマとして)成り立つ:
a≦b ∧ b≦a → a=b a≦b ∧ b≦c → a≦c (註) 厳密に言うとつぎのようになる。即ち,T' の変項記号a,bに対し,二つの記号列:
a≦b  の二つの記号列で置換する。この置換によって得られる記号列を,それぞれ φ ,ψと名付けるとしよう。 φ は の二つの記号列で置換する。この置換によって得られる記号列を,それぞれ φ ,ψと名付けるとしよう。 φ は  の一つの記号列(文)── の一つの記号列(文)── 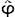 と名付ける──の簡略表記である。このとき,ψを と名付ける──の簡略表記である。このとき,ψを 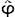 の簡略表記とする。 の簡略表記とする。
10 理論の形式化の例──自然数論 理論の形式化の例として,自然数論の形式化──形式的自然数論による非形式的自然数論の表現──を示す。 10.1 自然数論の形式化の論述 非形式的自然数論Tと形式的自然数論  は,それぞれある一定の論述を生成するシステムである。そして,このTと は,それぞれある一定の論述を生成するシステムである。そして,このTと  を対象化して示す論述は,T, を対象化して示す論述は,T,  とは別の或る理論T' が生成するところのものである。 とは別の或る理論T' が生成するところのものである。
T' は, " φ は  の定理", " φ はTの定理" の表現として,それぞれ の定理", " φ はTの定理" の表現として,それぞれ  φ , φ ,  φ を用いるものとする(註)。 φ を用いるものとする(註)。
T' は,Tを含んでいるものとする。したがって,T' の論述の中では,Tの文 φ に対する二つのT' の文としての  φ と φ は,互いに置換可能である。 φ と φ は,互いに置換可能である。
(註) 記号  を,ここでは記号 を,ここでは記号 と区別するためだけに用いる。(記号 と区別するためだけに用いる。(記号  のこのような使用は,通常のものではない。) のこのような使用は,通常のものではない。)
10.2自然数の表現 自然数 0,1,2,・・・・を,われわれは理論T' において理解している。そしてこの理解されている 0,1,2,・・・・は,理論Tの中の対象である。 "形式的自然数論による非形式的自然数論の表現" の主題に対し,われわれは,0,0' ,0",・・・・を,  の対象によるTの対象 0,1,2,・・・・の表現と定めることから出発する。 の対象によるTの対象 0,1,2,・・・・の表現と定めることから出発する。
以下,単に "自然数" と言うとき,それはTの対象としての自然数のことであるとする。また,表現の簡単のために,自然数nの表現になる  の自然数を, の自然数を, 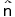 で表わすとしよう。即ち, で表わすとしよう。即ち,
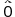 =0, =0,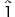 =0' , =0' ,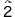 =0″,・・・・ =0″,・・・・
10.3 関係の表現可能性 Tの式 φ に対し,これの否定を〜 φ で表わす。 Tにおけるk項関係 R(x1,x2,・・・・,xk) が,  の式 の式 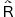 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k)) (註1) によって,数に関して表現可能(numeralwise expressible)であるとは,任意の自然数n1,n2,・・・・,nkに対して (ξ(1,1),ξ(1,2),・・・・,ξ(1,k)) (註1) によって,数に関して表現可能(numeralwise expressible)であるとは,任意の自然数n1,n2,・・・・,nkに対して
 R(n1,n2,・・・・,nk) ならば R(n1,n2,・・・・,nk) ならば
 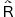 ( ( 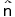 1, 1,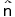 2,・・・・, 2,・・・・,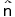 k) (註2) k) (註2)
(2)  〜R(n1,n2,・・・・,nk) ならば 〜R(n1,n2,・・・・,nk) ならば
 ¬ ¬ 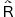 ( (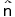 1, 1,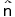 2,・・・・, 2,・・・・,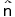 k) k)
以下,言い回しの簡単のために, "数に関して表現可能" を単に "表現可能" と言う。 (註) ここで表現 " 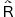 (ξ(1,1),ξ(1,2),・・・・,ξ(1,n))" は, (ξ(1,1),ξ(1,2),・・・・,ξ(1,n))" は,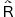 が,それの自由変数がξ(1,1),ξ(1,2),・・・・,ξ(1,n)の中にあるような一つの式の名であることを意味する。 が,それの自由変数がξ(1,1),ξ(1,2),・・・・,ξ(1,n)の中にあるような一つの式の名であることを意味する。
10.4 表現可能な関係の例 (註1) 関係x=yは,式ξ(1,1)=ξ(1,2)(厳密には,この形に簡略表記される前の式)に表現される。 関係x≦yは,式ξ(1,1)≦ξ(1,2)(厳密には,この形に簡略表記される前の式)に表現される。 k項関係 R(x1,x2,・・・・,xk) が,式 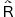 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k))
によって表現されれば,k−1項関係
R(x1,x1,x3,・・・・,xk)
は,式 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k))
によって表現されれば,k−1項関係
R(x1,x1,x3,・・・・,xk)
は,式
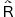 (ξ(1,1),ξ(1,1),ξ(1,3),・・・・,ξ(1,k))
によって表現される (註2)。 (ξ(1,1),ξ(1,1),ξ(1,3),・・・・,ξ(1,k))
によって表現される (註2)。
関係Rが式 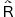 で表現されれば,関係〜Rは式 ¬ で表現されれば,関係〜Rは式 ¬ 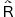 で表現される。 で表現される。
関係R,Sがそれぞれ式 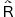 , , 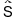 で表現されれば,関係 で表現されれば,関係
RならばS, RとSは同値
関係 R(x1,x2,・・・・,xk),y) が,式 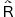 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k),ξ(1,m))(k<m)
によって表現されれば,自然数nに対し,関係 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k),ξ(1,m))(k<m)
によって表現されれば,自然数nに対し,関係
R(x1,x2,・・・・,xk),y)
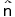 → →
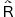 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k),ξ(1,m))) (ξ(1,1),ξ(1,2),・・・・,ξ(1,k),ξ(1,m)))
R(x1,x2,・・・・,xk),y)
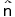 ∧ ∧
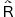 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k),ξ(1,m))) (ξ(1,1),ξ(1,2),・・・・,ξ(1,k),ξ(1,m)))
(註1) 前原昭二: "数学基礎論入門(基礎数学シリーズ26)" (朝倉書店,1977),pp.102-106. (註2) R(x1,x1,x3,・・・・,xk)は,R(x1,x2,・・・・,xk)の中のx2をx1で置き換えて得られる式を表わし, 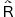 (ξ(1,1),ξ(1,1),ξ(1,3),・・・・,ξ(1,k))
は, (ξ(1,1),ξ(1,1),ξ(1,3),・・・・,ξ(1,k))
は,
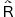 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k))
の中のξ(1,2)をξ(1,1)で置き換えて得られる式を表わす。 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k))
の中のξ(1,2)をξ(1,1)で置き換えて得られる式を表わす。
10.5 関数の表現可能性 Tにおけるk変項関数 f(x1,x2,・・・・,xk) が,  の項 の項
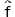 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k)) (註1)
によって,数に関して表現可能(numeralwise expressible)であるとは,任意の自然数n1,n2,・・・・,nk,mに対して (ξ(1,1),ξ(1,2),・・・・,ξ(1,k)) (註1)
によって,数に関して表現可能(numeralwise expressible)であるとは,任意の自然数n1,n2,・・・・,nk,mに対して
 f(n1,n2,・・・・,nk)=m ならば f(n1,n2,・・・・,nk)=m ならば
 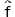 ( (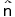 1, 1,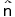 2,・・・・, 2,・・・・,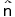 k)= k)=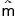 (註2) (註2)
以下,言い回しの簡単のために, "数に関して表現可能" を単に "表現可能" と言う。 (註) ここで表現 " 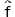 (ξ(1,1),ξ(1,2),・・・・,ξ(1,n))" は, (ξ(1,1),ξ(1,2),・・・・,ξ(1,n))" は,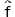 が,それの自由変数がξ(1,1),ξ(1,2),・・・・,ξ(1,n)の中にあるような一つの項の名であることを意味する。 が,それの自由変数がξ(1,1),ξ(1,2),・・・・,ξ(1,n)の中にあるような一つの項の名であることを意味する。
10.6 表現可能な関数の例 (註1) 関数x+1は,項ξ(1,1)' で表現される。 関数x( "恒等写像")は,項ξ(1,1)で表現される。 定数k( "定値関数")は,項(自然数) 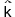 で表現される。 で表現される。
k変項関数f(x1,x2,・・・・,xk)が,項 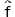 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k))によって表現されれば,k−1変項関数f(x1,x1,x3,・・・・,xk)は,項 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k))によって表現されれば,k−1変項関数f(x1,x1,x3,・・・・,xk)は,項
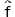 (ξ(1,1),ξ(1,1),ξ(1,3),・・・・,ξ(1,k))によって表現される (註2)。 (ξ(1,1),ξ(1,1),ξ(1,3),・・・・,ξ(1,k))によって表現される (註2)。
関数f(x1,x2,・・・・,xk)が,項 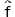 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k))によって表現され,関数g(y,z1,z2,・・・・,zp)が,項 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k))によって表現され,関数g(y,z1,z2,・・・・,zp)が,項
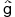 (ξ(1,m),ξ(1,k+1),ξ(1,k+2),・・・・,ξ(1,k+p)) (註3)(m>k+p)によって表現されれば,関数 (ξ(1,m),ξ(1,k+1),ξ(1,k+2),・・・・,ξ(1,k+p)) (註3)(m>k+p)によって表現されれば,関数
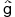 ( (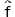 (ξ(1,1),・・・・,ξ(1,k)), (ξ(1,1),・・・・,ξ(1,k)),
ξ(1,k+1),・・・・,ξ(1,k+p)) (註1) 前原昭二: "数学基礎論入門(基礎数学シリーズ26)" (朝倉書店,1977),pp.107-109. (註2) f(x1,x1,x3,・・・・,xk)は,f(x1,x2,・・・・,xk)の中のx2をx1で置き換えて得られる式を表わし, 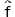 (ξ(1,1),ξ(1,1),ξ(1,3),・・・・,ξ(1,k)) は, (ξ(1,1),ξ(1,1),ξ(1,3),・・・・,ξ(1,k)) は,
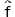 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k)) の中のξ(1,2)をξ(1,1)で置き換えて得られる式を表わす。 (ξ(1,1),ξ(1,2),・・・・,ξ(1,k)) の中のξ(1,2)をξ(1,1)で置き換えて得られる式を表わす。
(註3) ここで "ξ(1,k+i)" は,k+i=jのときのξ(1,j)と解する。 |