11.1 存在論 11.1.1 存在の非在と,存在の仮構 いま,例として,“机”という存在を考えてみる。このときわれわれは,差し当たって《何故それは“机”でなければならないか?》のように疑うことができる。しかしさらに,“実在”としてのそれさえ,疑うことができる。実際,“実在”として突き詰めて考えるとき(例えば,限りなく微視的に考えるとき),“机”は無化してしまう。結局,“机”は非在である。 一般に,ひとは名“・・・・”(例えば,“机”)によって存在を対象化するが,語“・・・・”に対応しているのは,非在である。したがって,ひとは語“・・・・”によって存在を仮構していることになる。 “存在の仮構”のように言うとき,ひとはつぎのように反論したくなるかも知れない。即ち,
この反論に対して,われわれはつぎのように答えることになる。即ち,〈命名以前〉は語に対応すべき存在の土台ではあっても,語に対応すべき存在そのものではない。 実際,例えば“机”について言えば,〈“机”以前〉が“机”である必要はない。 “対応する存在”が語“・・・・”の存在理由になるのではない。語“・・・・”の用途が語“・・・・”の存在理由である。そこで,語“・・・・”について考えるとは,これの用途を考えることである。《語“・・・・”に対応する存在は何か》というように考えることではない。われわれは,語“・・・・”に対して“存在との対応”を発想する古い体質と,決別しなければならない。 語“・・・・”の用途は,単一ではない──命名,存在の仮構,等々。 11.1.2 存在論の可能性 文字通りの存在論は,あり得ない。“存在”として存在するものは無いからである。“存在”はわれわれによって導入されたのであり,そしてわれわれの導入による“存在”は,非在である。 “存在論”というスタンスそのものが,誤っている。 “存在”の語を冠する論としてあり得るのは,存在導入/仮構の論,即ち,
11.1.3 存在のフィクションの用途 思考がことばによる思考に他ならないことにより,われわれは,“イデア”の発想に慣らされている。例えば,“異なる実在に同じモノ/コトが読まれる”という言い方に,抵抗を感じない。 “イデア”は,存在論的にではなく,方法論的に主題化されるべきである。即ち,“この方法は必要か否か,利点は何か”という具合に。 “イデア”の方法は,原理的には,これ無しで済ませなくはない。しかし,実際上,これ無しで済ませることはできない。 例えば,“紙に書かれた文字Aも,壁に描かれた文字Aも,ともに文字A!”であることを,われわれは“われわれの傾性(身体の傾向)”によって説明することができる。そしてこのようにすることで,“文字A”に関する存在のフィクションを退けることができる。 しかし,事態を傾性の事実として語ることは,著しく煩瑣なものになる。(端的に“文字A”を言い出すことができなくなった情況を想像してみよ。) さらに,存在のフィクションは,言語運用を軽快にするための方便としてのみ合理化されるのではない。“計算”という重要な用途がある。事態に対し存在のフィクションがつくられ,このフィクションの上で計算がなされ,そして計算結果が事態に解釈される。 そこでわれわれは,有用性の観点から存在のフィクションを用いることになる。フィクションであることを明記しつつ,また,存在のフィクションは傾性の事実へとつねに読み換えられるという認識に立って,存在のフィクションを用いるのである。 11.2 言語の存在論 11.2.1 “現象を欠く言語” われわれは,言語の規定を生成文法の規定に代え,特に,“言語”に対する“文法によって生成される文全体の集合”の定義を退けた((1), §2.1)。しかし,これは妥当なのか? “人が言語運用を一時停止するとき,言語は存在しなくなるのか,それとも存在し続けるのか?”というように自問してみよう。 “存在しなくなる”と答えるとき,言語は現象(出来事)のように考えられている。“存在し続ける”と答えるとき,言語は現象(出来事)の潜在性のように考えられている。 文は,文法の現象と見ることができ,文法は,文の潜在性と見ることができる。したがって,言語に対する“文が構成するところのもの”と“文法そのもの”の二つの見方は,それぞれ“現象”と“現象の潜在性”の見方と対応している。 われわれは,“言語”を“文法そのもの"/“現象の潜在性”として定義した。何故,“文が構成するところのもの"/“現象”として定義しなかったのか。 確かに,記号や文生成規則は,はじめ,言語現象の観察を通じてわれわれの対象になった。しかし,言語の意味は,経緯の前後関係で定まるのではない。 問題の中心は,《言語にとって現象──即ち,言語現象──は必要か?》ということである。必要ということにすれば,《言語であるためには,どのような現象が必要か?》のように問題が進む。 “現象は必要か?”の問いへの答えは,“必要でない!”か,“必要,しかもすべての現象が必要!”,でなければならない。単に,《中間ではあり得ない;何故ならどの中間に対してもわれわれはそれを特権化する理由をもてないから》という理由で。 さてわれわれは,《言語であるためにはすべての現象が必要》の立場を選ぼうとするか?選ばぬであろう。言語を語るために“すべての現象”への考慮が必要だと思ったことはないし,またこのような考慮はしようとしてもできることではないから。(そもそも,それは一体どのような考慮か?) 残された選択肢は,《言語にとって現象は必要でない!》である。 “生成文法”を使って文を実際に生成するということは,〈言語の構成〉の要素にはない。このようなデモンストレーションは,余計なサービスであり,要求されていない。言語は,文のデモンストレーションなしに既に言語でなければならない。──《デモンストレーションの或る段階で言語が成立する》という事態を認めることのできないわれわれの結論は,こうであるしかない。 われわれは,“言語”を“現象を欠く言語”として対象化したのである。 11.2.2 文法の実体化──“言語能力” われわれは,“言語”を文法のことであるとした。特に,それは現象を欠く。 “現象を欠く言語”の概念は,一見,途方もないフィクションのように感じられる。しかしそれは,“言語能力”へと実体化できるような具合になっている。実際,文生成の潜在性をわれわれの身体性として考えるとき,これまで“言語能力”の語で示唆されてきたところのもの(註1)がこの身体性にあたる。 こうして,言語は現象を欠くが,実体を欠くわけではない。言語は現象を欠くが,現前する。即ち,われわれにおいて現前する。 言語が存在するために現象は要らない。特に,すべての人が黙したとしても言語は存在している。しかし,人がいなくなるとき,言語もなくなる。 文法の定義は,“言語能力”の記述と見なせる(註2)。(実際,チョムスキーはこの立場で“生成変形文法”を発案した。) 形式的には,文法が文を生成する。実体的には,“言語能力”が文を生成する。 言語を人の身体性としての“能力"(“傾性”)に帰着させることは,同時に,“言語”の語の解消でもある。実際このとき,“言語運用”は“歩く”と同種であり,そして“歩く”を“歩行の運用”のような言い方をしないで済んでいるとなれば,“言語運用”の言い回しの中の“言語”の語は全然実効していないわけである。 (註1) “言語能力”の発想は,つぎのようになる:
(註2) ここで言う“記述”は,“能力”の操作的記述である。“操作的記述”と言うとき,われわれは“描写”をこれに対立させている。操作的に記述される“能力”は,〈機械〉にモデル化された“能力”である。 因に,“能力”のモデルの意義は,“能力”を〈機械〉化していることにあり,“能力”を描写することにはない。“能力”が為すことを(物理的あるいは論理的)機械で実現しようとしてつくられる機械が,“能力”モデルである。 11.3 理論の存在論 〈理論=論述生成システム〉の存在論は,〈言語=文生成システム〉の存在論(前節)と同型に展開される。 特に,“言語の現象としての文”の概念には,“理論の現象としての論述”の概念が対応する。 11.4 テクストの存在論 11.4.1 テクストの存在 テクストは,ひとの営みに示される。 テクストは何がしかの実在(印刷物,音波,等々)を土台にしている。しかし,この実在にプラスされる何かという形で,テクストが存在しているのではない。(勿論,この実在がテクストなのでもない。)テクストは,“テクストの土台”たる実在をめぐるひとの営みに示される。 即ち,或る仕方で或る対象が扱われているとき,われわれはそこにテクストがあると見なすのである。 例えば,ひとが石を“読んでいる”とき,われわれはその石においてテクストが存在していると見なす。ひとが石に腰掛けているとき,その石においてテクストが存在しているとは,考えない。 11.4.2 テクストの共同主観性 テクストは,共同主観(共同幻想)である。 われわれは,テクストに規範を見出せる。この事実は,テクストが共同主観であることの含意である。 “規範”は,“書き方”──記述/表示の媒体,様式(文の終了を示す方法,推論を表わす文の列の書き方,文や絵の引用/参照/指示形式,等)──および“読み方”の形で,主題化される。 11.4.3 テクストの現前態 テクストtがそこにおいて対象化されているところの“実在”を,tの現前態と呼び,記号 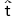 で表わすことにする。 で表わすことにする。
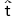 に対して差し当たり持たれるイメージは,“tの媒体(メディア)”である。実際, に対して差し当たり持たれるイメージは,“tの媒体(メディア)”である。実際,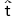 に対しては,“音声になったt”とか“紙に書かれたt”のような理解で十分な場合もある。しかし,“状況”とも言うべき広い意味で──“或る状況下で,或る仕草で渡された紙に書かれたt”といった具合に── に対しては,“音声になったt”とか“紙に書かれたt”のような理解で十分な場合もある。しかし,“状況”とも言うべき広い意味で──“或る状況下で,或る仕草で渡された紙に書かれたt”といった具合に──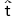 を考えねばならない場合もある。 を考えねばならない場合もある。
 の定義は,決定的に曖昧である。実際,“実在” の定義は,決定的に曖昧である。実際,“実在” は,われわれの判断(主観性)としてある。〈事実〉(客観性)としてあるのではない。 は,われわれの判断(主観性)としてある。〈事実〉(客観性)としてあるのではない。
われわれは,出来れば,  なしで,単に“テクストt”と言って済ませたいのである。しかし,“テクストt”という事態は,存在しないのである。(例えば,《コンピュータにキーボードから命令を入力するとき,“テクストt”という事態は何か?》と考えてみよ。) なしで,単に“テクストt”と言って済ませたいのである。しかし,“テクストt”という事態は,存在しないのである。(例えば,《コンピュータにキーボードから命令を入力するとき,“テクストt”という事態は何か?》と考えてみよ。)
“機械Mに対するテクストt”と言うとき,われわれは既に,Mに対してtが現前する形態を一つ念頭においているのである。その形態は,“単一のもの”と意識されている場合もあるし,“一定の枠内のもの”と意識されている場合もある。 “一定の枠内のもの”の意識は,例えば,つぎのような問題意識によっている: 《われわれが“テクストt”と捉えるものののMにとっての意味は,tがどのような媒体にのせられるかということで左右される》 12 意味 12.1 テクストの意味 12.1.1 テクストの意味 われわれは“意味”を,“テクストの意味”のことであるとする。 一つのテクストtの意味は,われわれが“主体M”として任意に想定するものそれぞれにとってのtの意味である。そして,tのMにとっての意味とは,tが契機(トリガー)になってMにおいて生ずる事態eである。 ここでわれわれは,つぎの思いを形式化して述べているのである:《“ことばに対する何か”としてことばの意味があるのではない;人に対するトリガーとしてことばが機能し,そこで何かが展開されるとき,その展開されていることがこのことばの意味である。》 実際,人にとって意味のあるものは,それが契機になって人が何かをする/してしまうようになるところのものである。 テクストt,主体M,事態eは,いずれもわれわれの解釈(意識対象)である。“tが契機(トリガー)になってMにおいて生ずる事態e”は,これ全体,われわれの解釈である。 テクストt,主体M,事態eは,それぞれ,何かに対してわれわれがそのように対象化したところのものである。その何かを,われわれは普通“実在”ということばで表現している。 12.1.2 論述の意味 “テクストの意味”を前節のように定義したとき,“論述の意味”も定義されてしまったわけである。実際,われわれは,このことに留意した上で,“テクストの意味”を定義したのである。 論述tの意味は,やはり,主体Mに対するtの意味であり,そしてそれは,tが契機(トリガー)になってMにおいて生ずる事態のことである。 われわれは,“論述”を“正確”なものと考える。そしてここから,客観的な意味を想定したくなる。しかし,“論述”を“正確”なものにしているのは,客観的な意味ではなく,推論規則である。論述の生成に,意味は終始関係しない。 12.2 テクストの受容 いまわれわれは, “テクストtに関わるしかじかの状況の実現は,主体Mにおいて何らかの事態が生ずる契機として実効する” という認識をもっているとしよう。このとき,その“しかじかの状況の実現”を“tをMに受容(accept)させる”というように読み直し,“Mにおいて生ずる事態”を“tに対するMの反応”と読み直すことにする。 Mの意義は“テクストtの受容主体”となる。そして,“テクストtのMにとっての意味”が,“tに対するMの反応”という形で捉えられることになる。 12.3 “テクスト受容”に対する段階の発想 われわれは,テクストの受容に段階を考えたくなることがある。 特に,“入力されたテクストの受容”のような見方をしたくなることがある。 段階的受容の図式は,本質的なものではない。実際,全ての段階の通過を,改めて一つの受容と定義することができる。 段階的受容の発想については,差し当たり,二つの理由を考えることができる。 一つは,記述の都合からである。即ち,“受容”という事態の記述をし易くすることがねらいである。“記述しにくい局面を暗黙のものとして,記述の可能なところから始める”という方法論も,これに類する。 そしてもう一つは,“テクストの受容に程度を設けたい──テクストを受容可能/受容不可能の二値では片付けたくない”という意識である。言い換えると,“各段階について,そこではじめて受容を拒否されるテクストというものを問題化したい”という意識である。 受容の各段階の定義は,やはり,Mの反応によって定義するという形のものである他ない。即ち,“Mの或る反応を引き起こせたことが,この段階の通過を意味する”が,定義の形態である。 12.4 テクスト受容機械 12.4.1 テクスト受容機械 テクストの受容主体を一般的に考えるとき,それは〈機械〉である。 例えば,コンピュータ言語の上のコンピュータの操作において,コンピュータはテクスト受容主体である。“テクストのインプット”という視点において,ことばによって人に働きかけることとコンピュータを操ることは,同質のものになる。 “機械”の対象化は恣意である。 例えば,“テクストtを複数の媒体において受容できる一つの実在”と意識されるものに対して,
(2) “複数の機械の混在” (3) “一つの受容器をもつ一つの機械"(“受容器は一つで,受容される媒体は同質である”と考える) また,テクストtの受容を実現する《t(§11.4.3)と受容器の対応》も,自ずとそこに見えているといったものではない。ここにも判断の恣意性が入り込む余地はある。 例えば,発声されたテクストtを,考えてみよう。このとき,tを直ちに音声(空気の振動)とすることはできない。実際,例えば以下のようなものもtであってよいわけである(§14.6,(註3)):声帯の振動と口唇のある形からある形への継起的な変化,相手の鼓膜の振動,聴覚器官の振動,末梢神経細胞の励起,中枢神経細胞の励起。実際,これらはそれぞれ,tの媒体と受容器との対応を示している。 12.4.2 状態 われわれは,テクストtの受容機械Mに対し,〈状態〉というパラメータを考える。この意味は,“tに対するMの反応”は,専ら“或る状態qにあるときのMがtに対して示す反応e”として考えられる,ということである。 特に,tの意味は,機械[人]によって違うだけでなく,機械[人]の“虫の居所”によっても違ってくるのである。 12.5 反応の把捉 “反応e”の把捉には,“反応の終了”の把捉が含まれる。 反応の終了を知る方法が存在しないで,かつ反応の終了を判断することがある。この場合,“反応の終了”の兆候といったものが,実践的/経験的に知られているわけである。しかしこの判断は,本質的に〈賭け〉である。 12.6 意味の定義 機械Mによるテクストtの受容の概念が,“状態qのMによるtの受容”として,つぎのような形で定義されているとする:
状態qにあるMを,(M,q)で表わすことにしよう。 われわれは,“テクストの意味”を“機械Mに対するテクストtの意味”として考え,そして,“tに対するMの反応”と定義した。そこで,テクスト受容の概念が上のように定義されている場合の“テクストの意味”を,つぎのように定義する。 即ち,Mが状態qでtを受容して,状態q′に変わる(即ち,状態q′で停止する)とき,Mのこの状態変化の過程を,(M,q)に対するtの意味と定める。──われわれは,テクストの意味を,機械の最終状態で定義するのではなく,機械の状態の変化で定義する。即ち,結果で定義するのではなく,経過で定義する。 この場合の状態変化に対しては,連続的と離散的の二つの捉え方が考えられる。後者の場合,状態変化は状態の列 {qn|n=0,1,・・・・,n} ──但し,q=q0,qn=q′──で表現できる。 Mが状態qでtに対して反応し,しかも停止しない場合は,(M,q)に対しtの意味は決定しないと言うことにしよう。 また,テクストtが(M,q)の受容するものではないとき,即ち,tに対して(M,q)が反応しないとき,tは(M,q)に対して無意味であると言うことにする。さらに,Mのどの状態qに対してもtが(M,q)に関して無意味であるとき,tはMに関して無意味であると言うことにする。 “反応”の判断は,恣意による。実際,“反応しない”ことも,反応と見なせる。──この場合,tに対して(M,q)が“反応しない”ことは,(M,q)に対するtの意味である。 12.7 意味の決定問題 前節での“意味”の定義は,意味の決定問題を,機械の停止問題の形で,孕んでいる。 実際,“停止する/しない”は,事態を見守るという方法によっては判定できない。いま停止しているように見えても,いつか動き出すかも知れない。また,いま動いていても,いつか停止するかも知れない。このとき,われわれには,観察を打切ることが許されない。 前節の“意味”の定義は,“停止する/しない”を決定する方法が予め与えられていることを,前提にしている。──少なくとも“停止する”を決定する方法は,与えられているとしなければならない。 12.8 意味論 12.8.1 理論の意味論 “意味論”を,われわれは“理論の意味論”のことであるとする。そして,理論Tの意味論とは,Tの下にあるテクストの意味の論述であるとする。 さらにわれわれは,理論Tの意味論は,このようなものとして,一つの理論T′の下のテクストt′として実現されると考える。 12.8.2 辞書的意味論 12.8.2.1 辞書的意味論 t′の一つの形態は,辞書的意味論である。即ち,TのことばにT′のことばを対置する形の意味論である。 ここでは,Tの意味論をT′の意味論へと転化することが,Tの意味論になっている。したがって,辞書的意味論に対しては,問題を単に引き延ばしたに過ぎないという見方が立つ。 なお,“国語辞書”は,ここで定義した辞書的意味論ではない。それは,つぎに述べる語用論に近い。また,“説明の堂々巡り”に目をつぶれば,マクロ定義の一覧とも見なせる。マクロ定義の一覧としての“国語辞書”の用途は,長い記号列を短い記号列に置き換えることと,これの逆(オリジナルの再現)をすることの二つである。 12.8.2.2 生成変形文法のプラグマティックな読み換え 生成変形文法やそれの類縁(例えば,格文法)での意味論は,“辞書的意味論”である。そして実際,“生成”という枠組みの下では,意味論はこのような形でしかあり得ない。“意味”が最も根源的な形で主題化されている例を,われわれは後期ウィトゲンシュタインに見ることができるのであるが,このような“意味”は,生成変形文法では扱えないのである。文は素材から構築(生成)できるが,意味は構築(生成)できないからである。 しかしこのことで,生成変形文法の理論が捨てられるわけではないし,生成変形文法の意味論(特に,“意義素”のような発想)も捨てられるわけではない。 われわれは,ここではプラグマティズムにつく。理論に関しては,“それは正しいのか/誤っているのか?”ということは問題にならない。問題になるのは,専ら,“使えるか/使えないか?”ということである。 人工言語の構築をわれわれの目的に据えるとき,生成変形文法やそれの類縁は使えるのである。特に,人工言語の構築では意味も構築するより他ないのであり,そしてこの場合の意味構築の手法は,自ずと生成変形文法やそれの類縁の手法に限定されてしまうのである。 12.8.3 語用論 12.8.3.1 語用論 理論T′の下のテクストt′がTの意味論として閉じている──即ち,Tの意味論をT′の意味論へと転化するものではない──とき,その形態は語用論である。それは,Tのことばの使用場面と用法の記述──“しかじかの場面でしかじかのことばがしかじかのように用いられるとき,しかじかの結果が生じる”──を内容とするものである。 われわれは,語用論を意味論の本来の形態と見なす。実際,われわれがこれまで論じてきた“意味”の論述は,語用論になる。 12.8.3.2 自然言語の語用論 (われわれの作為になる人工言語ではなく)はじめからわれわれの環境になっている──われわれがその上で生かされている──自然言語の場合,語用論として述べられるものは,基本的に,“ことばは現にこのように使われている”──事例──である。 “何故現にこのように使われるか”が説明されることもあるが,それは,〈事実〉を述べているのではなく解釈を述べているのである。さらに,その解釈は──解釈一般について言えることであるが──それによる何がしかの効用(結局のところ,“計算にのる”という効用)を意識している故に,提示されたものなのである。 12.8.3.3 “使用”と“効果” 自然言語の主題の下に,意味を根柢的に問うとき,それは“ことばの使用”というより他に言いようがなくなる(ウィトゲンシュタイン)。 ひとはこのときにも,意味を,ことばの使用そのものではなく,ことばの使用が引き起こす効果のように考えたくなるかも知れない。しかし,現実の中のことばの使用において,ことばの使用とそれの効果を分けることはできない。(ことばの使用を,具体的に考えてみよ。) 人工言語の場合も,同じである。 ことばは,使用の効果が示されたことによって使用されたことになる。“効果が示されない使用”がそもそも背理であるという意味で,われわれは,使用と効果を切り離せないのである。 12.8.3.4 世界 語用論は,一つの世界Wにおける語用の論である。 テクストtに反応する機械Mと,テクストtをMに受容させる〈わたし〉は,Wの要素である。tがこのような仕方で現前していることも,Wの要素である。 語用論──世界Wにおける語用の論──は,世界Wの間接的な記述と見なせる。 12.9 モデル 12.9.1 “可能世界”の発想 “世界Wにおける語用の論”としての語用論も,一つのテクストtとしては,Wから独立している。そこで逆に,“この語用論を成立させる世界”の発想が立つ。 即ち,tをWの間接的な記述と見なしてきたわけであるが,ここでtの中の世界Wを世界変数と見なすのである。 語用論tが成立する世界を,tの可能世界(possible world)と呼ぶ。ここで,tが世界Xで成立するとは,tで述べられる語用の各々が,世界Xでの営みになっているということである。 われわれは“可能世界”の概念を“語用論の可能世界”として導入したが,これは,通常の導入──“理論の可能世界”としての導入──と異なるのではない。実際,語用論tは或る理論Tの意味論であるが,このとき,(“tで述べられる語用の各々が世界Xでの営みになっている”こととして定義される)“tの可能世界”と,通常の定義(“Tの命題の各々が世界Xで真”)による“理論Tの可能世界”は,意味において同じものになる。 12.9.2 モデル “可能世界”の概念の,数学的定式化が“モデル”である。 “モデル”は,もともと,形式的理論に対しそれの意味論が主題化できるように,ということで提起された概念である。そしてこれの発想は,意味を集合論的事実として扱おうというものである。肝心な点は意味が集合論的に扱えるようになるということである。(そして,形式的理論に対するモデルの導入は,この限りで任意である(註3)。) “理論のモデル(可能世界)”は,あくまでも数学的概念である。《“世界”を,集合を土台とする“世界”に限る》という意味で,そうなのである。“理論Tのモデル(可能世界)を求める”の主題に対して,われわれが生活しているこの“世界”をチェックし始めるような粗忽を,してはならない。 (註) 例えば,命題論理(を伴う理論と見なした理論)と述語論理(を伴う理論と見なした理論)とでは,導入されるモデルの形式は同じではない。 12.9.3 文の“真偽” 命題論理,述語論理を伴う理論の場合,モデルMの条件は,各文φについてそれの真偽が一意的に決まるようになることである。そしてこれは,“Mに関してφは真”が集合論的事実として定義されていることによって,達成されるのである──集合論が排中律の成立する世界であることが,ここで効かされている。 システムMがモデルであるための条件は,“Mに関してφは真”が集合的事実で特徴づけられていることである。システムMは,それを“モデル”と呼ぶ(僭称する)ことでモデルになるのではない。繰り返し強調するが,“Mに関してφは真”が集合的事実で特徴づけられていて,はじめてMはモデルとなる。 したがって,論理に対してそれのモデルを形式的に構成することは,決して自明なことではない。また,構成の仕方も,対象にしている形式論理の如何に応ずることになる。 “φはMで真(true)”を,M  φで表わす。M φで表わす。M φに対しては,“φはMで真”の言い方の他に,“φはMで成り立つ",“φはMで満たされる",“Mはφを満たす",“Mはφのモデル”といった言い方もしていく。また,M φに対しては,“φはMで真”の言い方の他に,“φはMで成り立つ",“φはMで満たされる",“Mはφを満たす",“Mはφのモデル”といった言い方もしていく。また,M φでないことに対し,“φはMで偽”という言い方をする。 φでないことに対し,“φはMで偽”という言い方をする。
命題論理,述語論理を伴う理論に対するモデルについては,M  φを特徴づける集合的事実の否定が,M φを特徴づける集合的事実の否定が,M ¬φを特徴づける集合的事実となることを,条件にする。したがって,M ¬φを特徴づける集合的事実となることを,条件にする。したがって,M φ(“φはMで真"),M φ(“φはMで真"),M ¬φ(“¬φはMで真")の一方,かつ一方のみが,成り立つ。──特に,“φはMで偽”と“¬φはMで真”が同値となり,“φはMで真”と“¬φはMで偽”が同値となる。 ¬φ(“¬φはMで真")の一方,かつ一方のみが,成り立つ。──特に,“φはMで偽”と“¬φはMで真”が同値となり,“φはMで真”と“¬φはMで偽”が同値となる。
Tの文の集合ΣとモデルMにおいて,任意のφ∈Σに対しM  φであるとき,ΣはMに対し充足可能(satisfiable)である,あるいは,MはΣのモデルである,と言う。またこのことを,M φであるとき,ΣはMに対し充足可能(satisfiable)である,あるいは,MはΣのモデルである,と言う。またこのことを,M Σと表わす。 Σと表わす。
12.9.4 モデルから導出される文の二分法 Tの各モデルMに対して,Tの文全体の集合Sから真理値集合{t(“真"),f(“偽")}への関数h(M)がつぎのように定義される: t (M  φのとき) φのとき)
h(M)(φ)= f (M  φでないとき) φでないとき)
12.9.5 充足可能性 12.9.5.1 充足可能性 Tの文φ[文の集合Σ]は,モデルをもつとき──即ち,TのモデルMでM  φ[M φ[M Σ]となるものが存在するとき──,充足可能(satisfiable)であると言う。 Σ]となるものが存在するとき──,充足可能(satisfiable)であると言う。
12.9.5.2 文から導出されるモデルの二分法 Tのモデル全体の集合Mが空でないと仮定する。 各文φからは,Mから集合{t(“真"),f(“偽")}への関数h(φ)がつぎのように定義される(註3): t (M  φのとき) φのとき)
h(φ)(M)= f (M  φでないとき) φでないとき)
(註) しかし,つぎのような言い方はナンセンスである(レトリックとしての使い途もない): “命題は,世界を二つのカテゴリー,即ち命題が真である世界と偽である世界,に分類するための原理となる。” 12.9.5.3 恒真文 Tのモデルが存在するという条件の下で,Tの文φに関する“恒真(valid)”の概念をつぎのように導入する。即ち,文φは,Tの任意のモデルに対し真であるとき,恒真であると言う。またこのことを  φで表わす。 φで表わす。
強調しておくが,文の恒真性は,それが属している言語にモデルが存在する限りにおいて,問題にすることができる。──いま,“Tのモデル全体の集合”を形式的に考えることにして,それをMとする。“  φ”の定義は, φ”の定義は,
“Mが空でないとき,Mの任意の要素Mに対してM  φ” φ”
ではない。実際,もしこれが“  φ”の定義なら,Mが空のときTの任意の文が恒真ということになる。われわれは,公理系の“完全性”や“無矛盾性”の概念と関連させて“恒真”の概念を考えようとするから,“Mが空のときTの任意の文が恒真”であるような“恒真”の概念は退けられる。 φ”の定義なら,Mが空のときTの任意の文が恒真ということになる。われわれは,公理系の“完全性”や“無矛盾性”の概念と関連させて“恒真”の概念を考えようとするから,“Mが空のときTの任意の文が恒真”であるような“恒真”の概念は退けられる。
12.9.5.4 公理系の健全性 理論Tにモデルが存在すると仮定する。 Tの公理系が健全(sound)であるとは,定理がすべて恒真であること(“証明可能な文は恒真")。 健全性は無矛盾性を導く(註1)。 公理系が健全であるためには,つぎのことが成り立っていれば十分(註2):
(2) 推論規則が恒真性を保存する. (註1) 公理系が健全であるとして,定理φに対し¬φが定理でないことを示す。φは恒真であるから,任意のモデルMに対し,φはMで真。そしてこのとき,¬φはMで偽。よって,¬φは恒真ではない。さらに,公理の健全性から,¬φは定理でない。 (註2) 定理φの証明の列:ψ0,ψ1,・・・・,ψn=φにおいて,各ψiは,公理であるか,ψj(j<i)から推論規則によって導かれた文。そこで,(1),(2) が成り立っていれば,nに関する帰納法により,ψn=φは恒真。 12.9.5.5 公理系の完全性 理論Tにモデルが存在すると仮定する。 Tの公理系が完全(complete)であるとは,すべての恒真な文が定理であること(“恒真な文は証明可能")。 13 テクスト受容機械 13.1 “人”のモデル化 “テクスト受容機械”を“テクストを受容する人”の一般化として考える必要はないが,この概念の導入において,《“テクストを受容する人”の一般化》は配慮される。 この一般化は,モデル化の発想で行なわれる。“人”は図式化されるのであり,模写されるのではない。 モデル化において,われわれはコンピュータからのアナロジーが役立てることにする。 13.2 テクスト受容機械に対する“ハードウェア”の解釈 13.2.1 ハード われわれは,テクスト受容機械とテクストの関係を,ハード(ウェア)とソフト(ウェア)の関係で捉えるとしよう。 特に,ハードに関するメモリ,演算ユニット,入出力装置,データバス,センサーといった概念を,テクスト受容機械の記述概念として用いることにする。 13.2.2 ハードの改良 ハードは,“先天性”のアナロジーに用いることができる。実際,一旦完成されたコンピュータは,成長しない。 一旦完成されたコンピュータに対し,これのハード的な能力(“潜在能力”)をさらに高めようとして行なえることは,部品の新バージョンのものへの交換か,新しい機器の付加である。 後者では,演算チップ,ROM,RAM,各種周辺機器(+インタフェース)が,付加される機器の例になる。 人の場合の“周辺機器/インターフェース”の例:〈視る〉に関しては,望遠鏡,顕微鏡,眼鏡等。 13.2.3 ソフト ソフトとは,ハードの性能を発現させるドライバの謂いである。 ハードの性能は,ソフトを通して,そしてこのことによってのみ,発現する。 ハードの性能は,《これこれの働きかけ(ドライバ)に対してはこれこれのように反応する》という形でのみ捉えられる。翻って,ハードの性能は将来遭遇するドライバに対して待機するところの潜性として解釈される。 ハードがハードであることを維持する機制と,ハードの能力を発現させるドライバの概念とを,区別しよう。 例えば,“食物=栄養の意義はハードの維持にあり,能力発現のドライバとしてではない”という具合に。 13.3 ハードウェアの状態 13.3.1 “ハード”と“状態” “ハード”と“ハードの状態”の概念は,区別される。 例:A,Bの二人に,一つの問題を出す。このとき,Aは自分で考えようとし,Bは教科書,参考書の中から解を求めようとする。さて,問題に対するAとBの対応の違いを,われわれはどのようなことばで説明しようとするか。
(2) 〈ハードの状態〉──(後天的)知識──からの説明:“Aは類似の問題を既に経験しており,一方Bにとってその問題ははじめて出会う種類のものである。” 13.3.2 知識 13.3.2.1 知識 テクスト受容機械に対して,知識の概念を導入する。 知識データは,ハードの一部になっている恒久的なものと(ROM上のデータ)と,ソフトによってつくられた非恒久的(註3)なもの(RAM上のデータ)の,二通りに考えられる。 これは,“先天性と後天性”の二分法にあたる。 (註) “非恒久的”とは言っても,恒久的に保存されることを妨げるものではない。“非恒久的”のここでの意味は,書き換え(特に,消去)可能ということである。 13.3.2.2 知識の条件 メモリにデータが書き込まれているということで,知識が成立するわけではない。知識が成立するためには,データ処理のメカニズムが加わらなければならない。 われわれは,むしろ逆の形で言うべきである。即ち,データ処理のメカニズムが,メモリ上の一定のデータを知識とし,残りを知識でないとする,と。 13.4 テクスト受容機械の評価 13.4.1 〈量〉評価と〈能力〉評価 テクスト受容機械に対する評価については,二つの形態が考えられる(但し,二分法ではない)。一つは,ハードとして評価するものである。もう一つは,しかじかのテクスト=ソフトに対する反応を評価するものである。 評価は,対象の相対化ある。一個の対象それのみの評価は,評価ではなく記述である。 “ハードとして評価する”とは,メモリの大きさ,演算の速さ,占有スペースといったことを項目に立てて,これを評価することである。評価されているのは〈量〉である。これに対し,“テクスト=ソフトに対する反応を評価する”の方は,〈能力〉の評価である。 〈量〉評価も,確かに〈能力〉評価の意識で行なわれている。それは,潜在性の評価として意味づけることができる。しかし,“潜在性”とは“何かに対する潜在性”のことであり,“何か”が現出したときの結果論に他ならない。 したがって,“各ソフトに関する〈能力〉評価は〈量〉評価から演繹される”ということが原理的に言える筈だとしても,〈能力〉評価を〈量〉評価に代えることはできない。 13.4.2 “量”と“能力” 前節では,《ソフトに対するハードの反応の評価を,ハードの能力の評価と見なす》という具合にして,“能力”の語を導入した。このときひとは,能力はソフトを“ものさし”にして測られる,のような言い回しをしたくなるかも知れない。そしてここから,〈量〉評価と〈能力〉評価の間に本質的な違いはないのではないか,というように考えるかも知れない。 このときの思考のギャップは,“ものさし",“測る”の比喩にある。 われわれの文脈では,“量”と“能力”の二語は,“量として解釈されている/されていない能力”のように出会う。このときの“量”の概念に曖昧なところはない。それは,代数的空間の一種として定義される。 “ソフトに対するハードの反応”が量に表現されるとき,そしてそのときに限り,ソフトに対する“ハードの能力を測るものさし”の比喩は妥当である。 13.4.3 “性質"と“能力” ソフトに対するハードの反応は,“ハードの身体性(性質)”とも読める。 “身体性”と読むとき,ソフトに対するハードの反応は,ハードが“してしまったこと”となる。これに対し,“能力”と読むときには,ハードが“できたこと”になる。 ソフトに対するハードの反応をハードの“能力”と読むか“身体性”と読むかは,ハードの反応に対する見方に〈価値〉の観点が入っているか入っていないかで,分かれる。 “身体性”の場合,ハードの反応に対する見方に〈価値〉の観点は入っていない。しかし,身体性自身の評価(身体性に対する見方に〈価値〉の観点が入っている)はあり得る。 実際,“身体性(性質)”にも“優劣”の概念は随伴している。例えば,“改善”を言うことができるという具合に。 13.4.4 能力評価 能力評価として,つぎの三形態を考える。
(2) 到達度の観点に立ったハードの反応の評価; (3) 能力表現の語による類型化. (1) は,ハードがしたことを“ハードができること”と読み換えるだけのものである。このタイプの能力評価は,“記述において主観を減らす具体的な方法がその都度立つ”という意味で,客観的である。 (2) は,或る言い回しで能力レベルを表現した上で,《ハードのしたことがそのレベルに到達している能力の発現と見なせるかどうか》を判定するものである。 (3)は,或る能力表現の語“・・・・”を含む“この能力は・・・・である”という言い回しで,能力評価するものである。これが能力評価になるのは,能力表現の語がもともと評価語だからである。 (3)は,(2)の特殊と見なせる。実際,(2)での能力評価の言い回しは,(1)に属する言い回しと(3)に属する言い回しを両極端とする。 (2)の場合,到達度がより操作的に定義されることが,(1)により近くなることを意味する。また,評価がより客観性に近づくことを意味する。実際,この場合,判断の規準を明示的に導入する方法が操作的定義なのである。 (3)での“この能力は・・・・である”の判断では,ひとは判断の規準をもっていない。ひとは実践的に,その事態を“・・・・”であると判断する。規準を問われれば何ごとかを言うかも知れないが,“問われれば何かを言う”ということ自体は,判断が実際規準に拠ってなされたということを意味するものではない。 13.4.5 能力の記述 13.4.5.1 ハードの記述 テクスト受容機械=ハードが,《テクストに対するハードの反応が,ハードから演繹的に説明可能》のレベルにおいて知られているとき,そのハードの記述は,間接的にハードの能力の記述になる。 13.4.5.2 ソフトに対するハードの反応の記述 ハードの能力の直接的記述は,ソフトに対するハードの反応の記述である。 13.4.6 テクスト受容能力 13.4.6.1 テクスト受容能力 テクスト=ソフトに対するハードの反応の段階的解釈(§ )には,能力の段階的解釈が応ずる。そしてこのとき,反応の端緒──“テクストを受容する/しない”──に対応する“端緒となる能力”として,テクスト受容能力が対象化されることになる。 13.4.6.2 テクスト理解 能力となった“テクスト受容”に対する言い回しは,“テクスト理解”である。テクストを受容したことがテクストを理解したこととされ,受容しなかったことが理解できなかったこととされる。 13.5 テクスト受容機械の類型 われわれは,テクスト受容機械について,つぎの三つの類型を立てることにする:手続き実行型,思考型,成長型。(三分法としてではない。) 13.6 手続き実行型テクスト受容機械 13.6.1 手続き実行型テクスト受容機械 受容するテクストが“手続き”であって,これを実行するところのテクスト受容機械を,手続き実行型と呼ぶことにする。 13.6.2 “規則に従う” “手続き”を“規則”と見なすこともできよう。但しこのとき,それは,従う/従わないの選択肢を無意味とするような規則でなければならない。 規則は,機械の〈意識〉に働きかけるのではなく,ただ機械の状態を変更する。機械の反応は,この状態変更の結果として現われるに過ぎない。即ち,機械は,ウィトゲンシュタインの言う意味で“規則に従う”のである:
理由ないし正当化を主題化するのは,機械ではなく,機械を対象化している第三者である。 “機械の〈意識〉に働きかける規則”には,意味の契機は存在しない。したがって,
自己撞着を起こしたのは,“規則”の概念ではない。あくまでも“機械の〈意識〉に働きかける規則”の概念である。テクスト=規則が“規則”であるのは,直接機械の状態を変更するものであることによってである。そして,このようなものとしてのテクスト=規則は,《行為を決定する》のである。 (註) “This was our paradox: no course of action could be determined by a rule, because every course of action can be made out to accord with the rule. The answer was: if everything can be made out to accord with the rule, then it can also be made out to conflict with it. And so there would be neither accord nor conflict here.” [Wittgenstein,L.,“Philosophical Investigations",Basil Blackwell,Oxford,1958,§201.] 13.6.3 コンピュータにおける“規則に従う” いま述べたことを,さらにパラフレーズしてみよう。 われわれは,“コンピュータに計算させる”という言い方をする。しかしコンピュータは,計算しているつもりで計算しているわけではない。さらに,規則に従っているつもりで規則に従っているわけではない。模式化して言うと,ちょうど,水が水路を流れるように,事態が進んでいるのである。 即ち,つぎのようになる。われわれは平板の上に水路の回路をつくり(システムプログラムおよび実行プログラムをコンピュータのメモリ上におく),一方のへりを持ち上げて平板を傾け,そして水路の入口に水を或る状態で注ぐ(インプット)。水は出口から或る状態で流れ出てくる(アウトプット)。 コンピュータのメモリ上に水路を実現し,水路の入口に水を置くのがわれわれの仕事である。後は,水が勝手に流れる。 水が水路の中を流れるのは,それ以外にはないからであり,判断して流れているのではない。水は流れるべくして流れたのである。水は,水路によって,現にあるように流れる(流れてしまう)。 水路は,水が流れる“規則”ではない。機械の状態である。 13.7 思考型テクスト受容機械 13.7.1 問題解決 “思考”を,ここでは“問題解決における思考”のこととし,そして,“問題”であると自らが判断したテクストを受容するテクスト受容機械を,思考型テクスト受容機械と定義する。 証明機械は,思考型テクスト受容機械の一つの例であり,それ自体一つの重要な主題をなす。 13.7.2 “問題” “問題”として受容されるテクスト──即ち,テクスト受容機械が“問題”と見なすテクスト──が,“問題”である。“問題”か否かは,テクスト受容機械に依存する。テクストそのものの性質として,“問題”か否かが決まるのでない。 例:機械Mにとって“問題”となるテクストtは,機械M′からは,易し過ぎる/難し過ぎる/ナンセンス/問題のように読めない/・・・・の理由から,“問題”にされない。 13.7.3 解を問う表現形式 問題は,問題の内容が分析されて問題になるわけではない。実際われわれは,多くの場合,《問題の内容を分析する前に,それが問題であることを知る》のである。 解を問う表現形式が先ず存在する。そして,われわれはこれによって問題であることを判断する。 例:“1+1=2?",“1+1=2を証明せよ。”は,解を問う表現形式により問題として受け取られる。 13.7.4 問題の把捉 問題は,先ず“問題”として受け止められる。そしてつぎに,どのような問題であるかの把捉に入る。 問題の把捉は,しばしば,“問題構造”とか“用語の意味”といったことばで導かれる。 13.7.5 問題の変形 13.7.5.1 問題の変形 問題解決の一つの形態として,《受け取った問題を別の問題へ変形して解く》の主題が立つ。このときの“変形”には,いくつかの変形の合成として解釈されるようなものも含まれる。 さらにこの主題の下に,変形の類型の主題が立つ。同値変形,還元(帰着),一般化/特殊化といったものが,変形の類型として挙げられる。 “問題の変形”についても,つぎの二つが区別される:
(2) 受け取った問題に対し,変形された問題を出力し,これを再び自分の入力にする. 13.7.5.2 “順思考・逆思考” 所謂“順思考・逆思考”は,“問題の変形”の下位主題と見なせる。 “順・逆”は,論理的概念である。それは,或る論理演算に関しての“順・逆”のことである。この論理演算の了解の上で,“順思考・逆思考”の判断がはじめて可能になる。 13.7.5.3 計算を目指す問題解決 推論のアルゴリズムや対象式の等値変形のアルゴリズム等の遂行に対して,通常“機械的処理”のことばが用いられる。いまこれを簡単に“計算”と呼ぶことにする。 問題解決(の図式)に
(2) “計算” このような問題解決に対して,“計算を目指す問題解決”の言い回しを用いるとしよう。 非常に多くの問題解決が,計算を目指す問題解決である。特に,“リアルな問題解決”の概念は,“計算(機械的処理)”の概念と対立しない。 “計算を目指す”については,計算を持つ理論が既に考えられている場合と,そうでない場合の二つが,区別される。例えば,線型代数の計算問題への問題変形の場合,線型代数は,前者では目的であり,後者では結果である。所謂“数学的問題解決”も,この二つの解釈が立つ。 13.7.6 “独創性” “独創的”とは,ノンカテゴリカルな仕方で価値を出力する機械を,褒めることばである。──これに対し,ノンカテゴリカルな仕方で非価値を出力する機械は,“狂っている”ということになる。 ここで,カテゴリカル/ノンカテゴリカルは,多勢をなす機械の身体性とそうでない機械の身体性を対立させるためのことばである。 13.8 成長型テクスト受容機械 13.8.1 自己評価 ここでは,“自己評価(自己否定)”を,自己能力の評価(否定)のことであるとし,さらに,“成長”を,“自己評価(自己否定)を契機とする自己成長”のことであるとする。 受容可能なテクストが変わることも,自己成長の内容になる。 以上の意味で成長するテクスト受容機械を,成長型テクスト受容機械と呼ぶことにする。 13.8.2 自己評価の構造 評価が対象の相対化である(§13.4.1)ということは,この場合,自己評価が自己の相対化であることを意味する。自己の相対化は,他者を自己化することによる。複数の自己の中の自己として,相対化されるわけである。言うまでもなく,自己化された他者は,他者そのものではない。 特に,自己評価は他者評価と表裏をなす。 自己評価は私的である。規準が対象化されていても,その規準は私的である。公的な規準も,私的な規準へと換えられる。 結果として,Aの自己評価とBがAに対して行なう他者評価がつぎのように食い違う:“あなたはできないと言うが,あなたはできているではないか!” 13.8.3 自己評価の機制 いま,自己評価の機制を,知識評価の場合で考えることにする。 われわれは既に“知識”を,“テクスト受容機械におけるメモリ上のデータと,それを知識として実現するデータ処理メカニズム”というようにモデル化した(§13.3.2)。この場合,機械の知識を見ているのは,われわれであって,機械自身ではない。 機械は,自分の知識を直接見てこれを評価するのではない。機械が評価の材料にするのは,“テクストに対する自分の反応”として認識したところのものである。 即ち,或るテクストに対して自分が或る反応をしたという事実を以って,自分はしかじかを知っている/知らないと判断する。 機械は,自分の中の〈知っている〉状態そのものを認めることはできない。〈知っている〉ことを検証する実践を通じて,この状態に自らが在ることを認めるのである。 13.8.4 他者評価の機制 他者評価も,自己評価と同様の機制のものになる。即ち,“テクストに対する他者の反応”として自分が認識したものを材料に,他者を評価する。 13.8.5 自己/他者評価の変化 成長に応じて,自己/他者評価も変わり得る。但し,評価対象の自己/他者が成長によって変化するということが,専ら理由になるのではない。 評価のシステムも変わり得る。何故なら,評価システムも身体性であり,そして成長とは身体性の成長のことであるから。──結局,評価は,変化が変化を評価するという図式になる。 例:かつての“できる”が“できない”になる。“できる/できない”の評価枠が無に帰してしまう。 13.8.6 “転移” 13.8.6.1 “転移”の概念 “転移”の概念は,つぎの言い回しに表現されるところのものである: “機械Mが問題x(問題の集合X)が解決できるように成長していれば,Mは同時に形式Sの問題が解決できるように成長していることになる。” 例:“赤のおはじきが数えられるようになれば,同時に,どんな色のおはじきも数えられるようになっている。” 13.8.6.2 “転移”を問題化する立場 “転移”を問題化する立場として,二つ考えよう。一つは,機械Mに指導しようとする立場,そしてもう一つは,機械Mを説明しようとする立場である。 Mに指導しようとする立場では,x(X)とSの関係は,Sに対するx(X)である。実際,Sに対しつぎのような考えから求められたのがx(X)である:
指導は最も効率的に行ないたい; 《それが解ければ形式Sの問題も解けるようになる》の条件を満たす問題で,最も簡単なものを求めよう; 問題の集合が必要なときには,必要最少限の数にとどめよう。 Mを説明しようとする立場では,x(X)とSの関係は,x(X)に対するSである。実際, Mが問題x(問題の集合X)を解決できるようになれば,形式Sの問題も解決できるようになっているということに説明を与えることが,この場合の主題である。 13.8.7 問題形式 われわれは,“問題形式”が何かを述べずに,このことばを用いて“転移”について述べてきた。 問題形式は,機械によって定義(説明)される概念である。それは,つぎのように定義される: 問題xの形式がSであるとは,xが機械Mで解かれることである. 問題形式を説明する機械の実践は,説明されるかも知れないし,ここで説明が終るかも知れない。説明されるにしても,その説明は別の機械の実践に遡行するのみである。 問題の同類性,類似性も,問題形式によって説明されるものとして,結局,ある機械の実践による説明のところで,説明が尽きる。 例:“a+1=2となるa?”と“b+1=2となるb?”は,われわれにとって同じ形式の問題になるという理由で,同じ形式の問題である。われわれにとって同じ形式の問題になることの説明は,結局,〈われわれのしてしまうこと〉による説明のところで尽きる。 問題形式が機械の実践で説明されるところのものであるということは,また,問題形式が結果論であることを意味している。同じ意味で,問題の同類性,類似性も,結果論である。 実際,“問題形式",“問題の同類性/類似性”は,問題がどのように解かれるかを知っていて,はじめて言えることである。“同じように解決される”──これの定式化が“ある機械Mによって解決される”であった──とき,問題は同類/類似であるということになる。 14 テクスト使用 14.1 手段としてのテクスト テクスト受容機械にテクストを受容させる行為が,テクスト使用である。 テクスト使用には目的がある。逆に,テクストは或る目的達成のために使用される手段である。 われわれは,テクストを考えるときは,つねに,“ある目的をもって使われるテクスト”として考えることにする(註3)。 したがって特に,(“先ずテクストがある”という立場で発せられるところの)“テクストの目的は?”のような問題は,初めから問題として起こらない。われわれの立場では,先ず目的があり,その目的の遂行のために或るテクストが後続して起こる。 (註) “目的がある/ない”と“生きている/死んでいる”を区別すること。ここで,“かつては目的があって使われたが,いまは使う目的がなくなってしまったテクスト”が,“死んだテクスト”である。 14.2 テクスト使用のカテゴリー テクスト使用──テクストtをテクスト受容/出力機械Mに受容させる行為──の目的を,つぎの四通りに考える。
(2) 所期の状態をMにもたらす; (3) Mが何を出力するかを見る; (4) Mがどんな状態になるかを見る. そして,(1)/(2)を目的とするテクスト使用を“企図”と呼び,(3)/(4)を目的とするテクスト使用を“試験”と呼ぶことにする。 そこで,例えば“依頼",“指示",“命令”は (1)を目的とする企図,“告知",“説明",“教唆”は (2)を目的とする企図,ということにそれぞれなる。 14.3 コミュニケーション 機械間での企図のやりとりを,“コミュニケーション”と定義する。 14.4 ことばの使用に関する“正しさ” 14.4.1 結果論としての“正しさ” ことばの或る使用が目的に沿うものか否かは,そのことばを分析してわかることではない。用例集によって,決まるわけでもない──現前の事態を用例集の中の一つの場面と見なし,用例集が示唆している通りにことばを使用しても,思う通りに事が進行するとは限らない。 即ち,原理的には,ことばの或る使用が目的に沿うものか否かは,予め知ることはできない。ことばの使用は,〈賭け〉である(ウィトゲンシュタイン)。 ことばの使用の“正しさ”の定義は,“結果として思う通りに事が進む”である。ことばの使用についての“正しい/正しくない”は,結果として言えるのみである。 14.4.2 システムの事態としての“正しさ” ことばの使用の“正しさ”は,ことばの使用がもたらす事態で評価される。そしてその事態は,テクスト受容/出力機械の関係システム──相互に他者として相手に関わる関係のシステム──の事態である。 14.5 他者 14.5.1 他者 “テクストtによるコミュニケーション”の成立──自分にとっての成立──は,つぎの二つが順次成立することでなる:
(2) 相手が所期の反応を示すこと. 相手に対し“tによるコミュニケーションの成立に確信がもてない”という感想がもたれる場合がある。このとき,tによるコミュニケーションに関して相手は自分の他者である,という言い方をするとしよう。 “他者”は,“他人”のことではない。“他者”ということばを,ここでは,《“自分に疎遠なもの”として逆に“自己疎外の契機”であるところのもの一般》の意味で導入する。 さて,コミュニケーション成立の内容 (1),(2)に応じて,他者はつぎの二様の位相で考えられる:
(2) テクストtを受容し反応するが,反応が所期のものではない. (1)のような他者に対する特徴的な呼び名が,“赤ん坊”あるいは“外人”である。また,(2)のような他者に対する特徴的な呼び名が,“子ども”あるいは“狂人”である。 コミュニケーションは,相手が他者でないことを願う〈賭け〉である。 “他者”と意識する相手への働きかけも,自分と相手の間に或る事態を引き起こすことを目的にしている。そして,他者が“他者”である所以は,この働きかけにおいてその目的が必ずしも実現されないということである。目的達成にリスクが伴わないような“他者”は,もともと他者ではなかったということになる。それは自分の延長に過ぎない。それは“道具”と呼ぶのがふさわしい。 他人も機械も,あるときは自分の延長(道具)となり,またあるときは他者となる。 14.5.2 コミュニケーションの構築 現前の他者に対しコミュニケーションを貫徹するためには,他者を誘導していく形のコミュニケーションの構築を図らなければならない。 この場合,“他者を誘導する”とは,他者の内部状態を変化させていくことである。 われわれは,コミュニケーションの失敗によって相手を知るようになる。そして相手を知ることで,コミュニケーションの方略が立つようになる。 14.6 “話されたことば” コミュニケーション(“相手に話す”)の現象的記述の中で,“話されたことば”はどのように記述されることになるであろうか? 先ず,現象としてのことばの記述は,テクスト(=記号列)の記述ではない。 実際,記号はフィクションである。(話されたことばの中に,記号は見えない!)また,《“話した”と自分が思っていることの記述は,現象の記述ではない》という意味でも,テクストの記述は現象の記述ではない。“話した”と思うことは,実際に“話した”ことにはならないからである。 “話されたことば”の条件は,相手のある反応Rのトリガーになっているということである。 しかし,Rのトリガーは,単一である必要はない。実際,Rのトリガーとしてわれわれが初めに考えたものTとRの関係は,つぎのような図式(註1)で考える方が自然である。即ち,Tが一つの事態を起こすトリガーになる;つぎに,後者がまた別の一つの事態を起こすトリガーになる;このパターンの繰り返し;そして最終的にRが現われる(註2)。そしてこの場合,TとRの間にある事態は,すべてRのトリガーである。 したがって,“話されたことば”とは,“Rの最初のトリガーになったもの”と意識されている事態のことであると言える(註3)。 (註1) この図式は,“相手”が機械である場合も含んだ一般的な図式になっている。 (註2) 例えば“ひとに話す”の場合,われわれはつぎのような図式を立てる。
(註3) 例えば,(註2)の図式を
また例えば,コンピュータのキーボード上のキーの押下がコンピュータ操作(“コンピュータに話す”)の端緒と意識される場合,それがコンピュータに“話されたことば”ということになる。 14.7 インタフェース 14.7.1 インタフェース 《自分が受容するテクストを“テクスト”──“理解の対象”──と認識する》は,テクスト受容機械の条件ではない。テクストの受容において,テクストは“理解”されるのではなく,単に受容されるのである。 したがって,機械Mの受容できないテクストからMが受容できるテクストへの変換は,“翻訳”ではない。 いま,テクスト出力機械M′,テクスト受容機械M,そしてM′とMの間で機能するテクスト変換装置Uに対し,UがMに装着されている状態を想定する。このとき,われわれはUを“M′に対するMのインタフェース”と呼ぶことにする。 
翻訳機はインタフェースの一種ということになる。 なお,Uを伴ったMは,改めて一つのテクスト受容機械M1と見なすことができる。M1は,M′の出力するテクストを直接受容できる機械となる。 14.7.2 インタフェース構築の理由 テクスト出力機械M′とテクスト受容機械Mに対し,Mの上にM′に対するインターフェースUを構築するのは,もう一つの機械W(特に,“われわれ”)である。 M,M′も,Wであり得る。 Wは,M′ が出力するテクストとMが受容できるテクストの両方の構造を知っていることになる。したがってWは,望めば,MとM′を仲介できるわけである。このような立場にあるWがUを構築しようとするのは,M′の出力するテクストが自動的にMに受容されるようにすることで,何がしかの利益を得ようとするためである。例えば,MとM′の仲介の労をとらずに済むようになるためである。 14.8 データ 14.8.1 データ “データ”は,使用テクストの見方であり,テクストの形態ではない。即ち,“処理の対象”と見られたテクストが,データである。 “処理の対象”の解釈は,恣意による。実際,すべてのテクストに対し,“データ”の見方が可能である。 テクストが“データ”のとき,テクスト受容機械は“データ処理機械”(さらに“計算機”)となる。 テクストtを“データ”と読むのは,tを受容する機械Mではなく,tとMを対象化している別の機械W(例えば“われわれ”)である。 Wは,テクストを〈何か〉のデータとして意識しつつ,処理(計算)はその〈何か〉から独立しているということを認識している,そういう主体である。実際,このような意識/認識において,テクストは“データ”になる。また,〈何か〉から独立しているが故に,その処理は“計算”なのである。 14.8.2 データ化の意義 データ処理が念頭にある限りで,データ化がある。データ形態が〈ことば〉であるとき,データ処理がことばの処理として行なわれることの利点が,予め見込まれていることになる。 対象をことばの形態にデータ化する行為が,“記述”である。記述は,データ処理としての〈ことばの処理〉を念頭においている。 “対象のデータ化”という言い方をしたが,“データ化以前の対象”の特定は,また“対象のデータ化”である。また,“対象"(“モノ",“コト")は,それをつきとめようとするときには,消えてしまう。パラドクスめいてくるが,“対象”は,つきとめようとしない限りで捉えられる。 “対象”については“意識対象”という言い回しを用いて表現するしかない。そこで,対象の記述は意識対象の記述である。そして意識対象の記述とは,意識対象に語あるいは文を対応させることである。 記述の意義を考えることは,この対応づけの意義を考えることである。そして,先に述べたように,〈データ化〉がこれの意義なのである。 計算の結果である語あるいは文に対し,われわれは何か或る対象を読もうとする。この結果,最初の対象から,新しい対象が計算によって導かれたことになる。 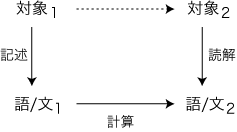
14.9 数学のテクストの使用 14.9.1 データ 数学のテクストの場合,データ処理は“数計算",“論理計算”であり,このように読まれた処理の対象が,データである。 なお,“数学のテクストの受容”の言い回しから先ずイメージされるものは“数学書を読む”であるが,このときの“数学書”のテクストとしての身分は,データである。 14.9.2 コミュニケーション 数学は,人と人の間のコミュニケーション言語にはなっていない。コミュニケーション言語として使われるのは,人とコンピュータの間においてである。 数学のどのようなテクストが,相手に何かをさせる/してもらうための手段になるか?そしてそれは,どのように使われたときか? われわれは,コンピュータのプログラムを,数学テクストがコミュニケーション手段になるときの形態と見なすことができる。 コンピュータのプログラミング言語(コンピュータに仕事をさせるために開発された人工言語)では,命令は,命令語を用いるか,関数に実引数を渡すという形で為される。さらに,命令語は関数の形でも実現される。そこで,一般に,《関数に実引数を渡す》を命令の形態とすることができる。 相手に何かをさせる/してもらうための数学テクストの形態を,これと同様のものと考えよう。即ち,《関数とこの関数に渡す実引数を相手に与える》を,命令(依頼)とする。 このときには,関数の構成法が命令の構成法の意味をもつことになる。 |