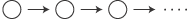
| Up | 2.1.2 “ペアノの公理”の読み方 | - |
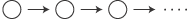
 である。そして先頭の項が1である。
である。そして先頭の項が1である。
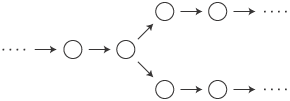
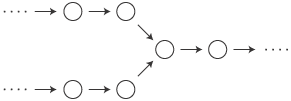
 が互いに独立した複数の系列で成るという状態である。しかしこの状態は,条件3°(註1)によって禁止されている。実際,
が互いに独立した複数の系列で成るという状態である。しかしこの状態は,条件3°(註1)によって禁止されている。実際,

 ′をとると,
′をとると,  ′は3°の中の
′は3°の中の  ′の条件を満たしているから
′の条件を満たしているから  ′=
′=  でなければならない。
でなければならない。
 は一本の系列でなければならないことになる。
は一本の系列でなければならないことになる。
 ─→
─→  を
を
| fn = | 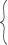
| fのn回の合成 (n>0) |
| 恒等関数 (n=0) |
 である(註3)。
である(註3)。
| (註1) | 条件3°は,“数学的帰納法の公理”と呼ばれる。
実際,命題関数P(x)に対する命題  ′={x│x ′={x│x  かつP(x)}とおいたときの命題 かつP(x)}とおいたときの命題
 ′= ′=  ” ” |
| (註2) | ここでの“整数n≧0”は,目下自然数を論じているところの言語(“メタ言語")に属する。したがって,後で,自然数の拡張としての整数が登場するが,循環論法ではない。 |
| (註3) | 条件3°の直接の適用。 |