Up

2.1.4 カテゴリカルな公理系

-

---

　われわれは自然数 を，色々あるものとしてではなく，ただ一つのものとして意識している。したがって，ペアノの公理による“自然数の定義”が真に自然数の定義になっているためには，それによって自然数が一意に定まるのでなければならない。
　ここで“ただ一つ”とは,“同型の意味でただ一つ”ということである。
　自然数の系の同型は，つぎのように定義する。即ち，ペアノの公理を満たす二つの系（ ,1,ｆ）と（ ,1,ｆ）が同型であるとは， と の間の１対１対応ｈ: ─→ で条件：

1°	ｈ(1) ＝ 1
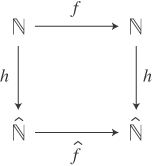
2°	つぎの図式は可換：

を満たすものが存在すること^(註))。そして実際，このようなｈは存在する──かつ

ｈ(fⁿ(1)) ＝ fⁿ(1)

で定義されるものに限る。
　一般に，ある公理系で定義されるところのものが“同型の意味で一つだけ”であるとき，その公理系は“カテゴリカル”であると言われる。ペアノの公理系は，カテゴリカルな公理系の一つの例になっている。

（註） “コピーｈ:（ ,1,ｆ）─→（ ,1,ｆ）”の概念の定式化は，このようになる。