 乽悢偲偼壗偐?乿傊偺摎偊 乽悢偲偼壗偐?乿傊偺摎偊
 偄傠偄傠側悢偑偮偔傜傟傞偟偔傒 偄傠偄傠側悢偑偮偔傜傟傞偟偔傒
 悢偼検偺斾 悢偼検偺斾
|



|
嬥戲戝妛嫵堢妛晹嫵壢嫵堢尋媶 no.26 (1990,7), pp.143-162.
| 嶼悢丒悢妛壢嫵嵽尋媶劅劅悢偺掕幃壔 |
媨丂壓丂丂塸丂柧
|
栚丂丂丂師
1 悢偺掕幃壔偺曽朄 2 悢偺帺屓姰寢揑掕幃壔

 偺掕媊劅劅乬儁傾僲偺岞棟乭 偺掕媊劅劅乬儁傾僲偺岞棟乭
2.1.2 乬儁傾僲偺岞棟乭偺撉傒曽 2.1.3  偺峔惉揑掕媊 偺峔惉揑掕媊
2.1.3.2 帺桼敿孮偐傜偺乬帺慠悢偺宯乭偺摫弌 2.1.4 僇僥僑儕僇儖側岞棟宯 2.1.5 弴彉娭學偺摫擖 2.1.6 壛朄偺摫擖 2.1.7 忔朄偺摫擖 2.1.8  偺峔憿 偺峔憿
2.2 悢偺奼挘 2.3 乬悢偺宯乭
2.3.2 悢偺宯偺峔憿 2.4  R R
 R偺掕媊 R偺掕媊
2.4.2 弴彉娭學偺摫擖 2.4.3 壛朄偺摫擖 2.4.4 忔朄偺摫擖 2.4.5  R偺峔憿 R偺峔憿
2.4.6  R偺拞傊偺 R偺拞傊偺 偺杽傔崬傒 偺杽傔崬傒
2.4.7 乬帺慠悢偺彍朄乭 2.4.8 乬傾儖僉儊僨僗偺岞棟乭 2.5  D乮亖惍悢偺宯 D乮亖惍悢偺宯 乯 乯
 D 偺掕媊 D 偺掕媊
2.5.2 弴彉娭學偺摫擖 2.5.3 壛朄偺摫擖 2.5.4 忔朄偺摫擖 2.5.5  D 偺峔憿 D 偺峔憿
2.5.6  D 偺拞傊偺 D 偺拞傊偺 偺杽傔崬傒 偺杽傔崬傒
2.5.7 乬帺慠悢偺尭朄乭 2.5.8 忔朄偺夝庍 2.6 (  D)R乮亖桳棟悢偺宯 D)R乮亖桳棟悢偺宯 乯 乯
 D)R偺掕媊 D)R偺掕媊
2.6.2 弴彉娭學偺摫擖 2.6.3 壛朄偺摫擖 2.6.4 忔朄偺摫擖 2.6.5 (  D)R偺峔憿 D)R偺峔憿
2.6.6 (  D)R偺拞傊偺 D)R偺拞傊偺 D 偺杽傔崬傒 D 偺杽傔崬傒
2.7 (  R)D R)D
 R)D偺掕媊 R)D偺掕媊
2.7.2 (  R)D偺拞傊偺 R)D偺拞傊偺 R偺杽傔崬傒 R偺杽傔崬傒
2.7.3 (  R)D偲( R)D偲( D)R偺摨宆惈 D)R偺摨宆惈
2.8 乬暵偠偨乭奼挘
 R)R偲 R)R偲 R偺摨宆惈 R偺摨宆惈
2.8.2 (  D)D偲 D)D偲 D偺摨宆惈 D偺摨宆惈
2.8.3 (((  R)D)R偲 R)D)R偲 RD偺摨宆惈 RD偺摨宆惈
2.8.4 ((  D)R)D偲 D)R)D偲 RD偺摨宆惈 RD偺摨宆惈
3 検偵悘敽偡傞悢 1
3.2 乬検乭偺奣擮偺椞暘 3.3 乬検乭偺堦斒揑宍幃 3.4 乬検乭偵懳偡傞嶰偮偺擇暘朄 3.5 撪嶼朄亄偑掕媊偝傟偰偄傞応崌
3.5.2 乬悢偺宯乭偲偟偰偺乮俻,亝,亄乯 3.5.3 乬悢偺宯乭偺峔惉偲偟偰偺乮俻,亝,亄乯偺峔惉 3.5.4 棧嶶検偐傜偺鈌枾検偺峔惉偲丆鈌枾検偐傜偺棧嶶検偺摫弌 3.5.5 乬斾乭偺宯 3.5.6 宯乮(俻,亝,亄),(N,亝,亄,亊),亊乯 3.5.7 乬嵎乭偺宯 3.5.8 宯乮(俻,亝),((俢,亝,亄),(N,亝,亄,亊),亊),亄乯 3.6 撪嶼朄亄偑掕媊偝傟偰偄側偄応崌
3.6.2 乬嵎乭偺宯
3.6.2.2 乮俻,亝乯偑鈌枾偺応崌 3.6.3 宯乮(俻,亝),((俢,亝,亄),(  DR,亝,亄,亊),亊),亄乯 DR,亝,亄,亊),亊),亄乯
3.7 検偺堦斒宍((俻,亝),((俢,亝,亄),(  DR,亝,亄,亊),亊),亄乯 DR,亝,亄,亊),亊),亄乯
|

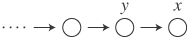

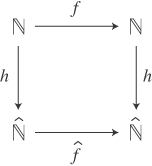
 倶
倶 倣亄倫亝値亄倫丏
倣亄倫亝値亄倫丏