Fのグラフ(左) とfのグラフ(右): 
このとき,
そこでこの操作ですが,考え方はつぎのようになります: 小学生はつぎのことができます: そこで,つぎのように近似してみます:
さらに,細かく区分して,近似 (直線と定値) をより精細にしてみます: 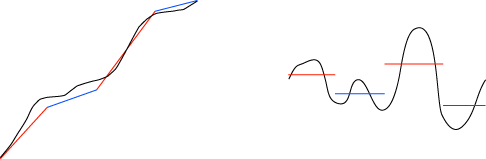

細かく区分するほど近似は精密を増し,もとのグラフがほとんど再現されるようになります:
ここでは,「F対f」を使って「微分・積分」の概念を導入しましたが,「微分・積分」の意味を一般的に述べると,つぎのようになります:
|
| Up | 関数グラフとしての曲線の形と各点での傾き |
Fのグラフ(左) とfのグラフ(右): 
このとき,
そこでこの操作ですが,考え方はつぎのようになります: 小学生はつぎのことができます: そこで,つぎのように近似してみます:
さらに,細かく区分して,近似 (直線と定値) をより精細にしてみます: 

細かく区分するほど近似は精密を増し,もとのグラフがほとんど再現されるようになります:
ここでは,「F対f」を使って「微分・積分」の概念を導入しましたが,「微分・積分」の意味を一般的に述べると,つぎのようになります:
|