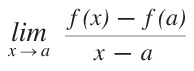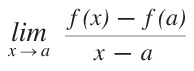Up 「微分」の定義  

  • 関数 f に対し，f の変化を表現する関数 f' を求めること (その内容) を，「f を微分する」と言います。
    そこで「f の変化の表現」ですが，これはつぎのように定めます：

    • 点Ｐにおいてなめらかな関数 f に対し，「Ｐにおける f の変化を表現する1次関数 (接線)」をつぎの条件によって定める：
      1. Ｐを通る
      2. Ｐにおけるｆの変化率を傾きとする

    • いたるところなめらかな関数 f に対し，「 f の変化を表現する関数 f' (f の導関数)」をつぎのように定義する：
        f'(x) ＝ 点(x, f(x)) におけるｆの変化率

  • 点Ｐにおいて「なめらか」とは，操作的には，点Ｐ (a, f(a)) におけるｆの変化率
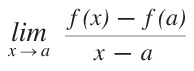
    が求まることです。そしてこのことは，ここで導入した「微分」の語を使えば，「微分可能」と言い換えられることになります。