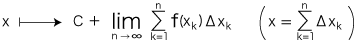
 この関数の意味) この関数の意味)
定義より,f の原始関数 F と定数 C に対し G(x) = F(x) + C で定義される関数 G は,f の原始関数になる。

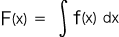
しかしこうすると,左辺の「x」が右辺には現れていない。 そこで,つぎの表現にする: 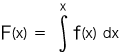
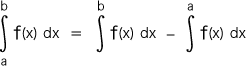
このとき,つぎが成り立っている: 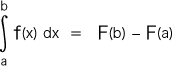
注意: |
| Up | 積分の記号法 | 作成: 2006-07-23 更新: 2007-10-31 |
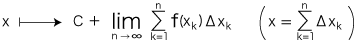
 この関数の意味) この関数の意味)
定義より,f の原始関数 F と定数 C に対し G(x) = F(x) + C で定義される関数 G は,f の原始関数になる。

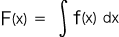
しかしこうすると,左辺の「x」が右辺には現れていない。 そこで,つぎの表現にする: 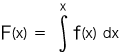
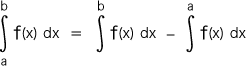
このとき,つぎが成り立っている: 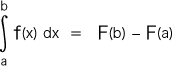
注意: |