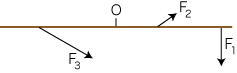
この回転運動は,ひとが座る位置とそのひとの体重によって,回転の向き・強さが違ってきます。 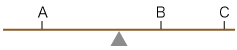
この回転の向き・強さを表すのに,「力のモーメント」という概念が導入されます。 力のモーメントの大きさは,回転の中心Oと力の作用点Pとの距離 d と,力の大きさ F の積で定義されます。 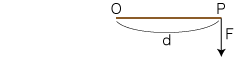
例えば,高校物理ですと,つぎのような具合に計算されます:
さて,高校数学の「力のモーメント」には,回転の向きが表現されていません。 また,力のモーメントは,実際問題として,複数の (作用点, 力) の組に対して考える必要が出てきます:
そこで「力のモーメントをどんなふうに定式化したら,回転の向きが表現され,そしてうまく計算できるようになるか?」という問題がもたれます。 そして,これの解答になったのが,力のモーメントを有向距離と力の外積 d×F で定義するというものです: 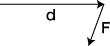
上の図 (*) の場合,右回転を起こすモーメント,左回転を起こすモーメントが,それぞれ手前から向こうに向かうベクトルと向こうから手前に向かうベクトルになり,これらのベクトルの和で,最終的なモーメント (回転の表現) が計算できることになります。 |