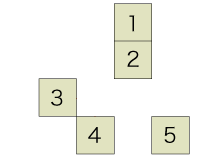
このとき,平板が傾かない位置に支点をもってくれば,その位置が正方形5枚の系の重心ということになります。 重心をGとし,正方形nの中心 (重心) をPn とします (n=1, 2, 3, 4, 5)。 各Pn には,同じ重力ベクトル F が作用しています。 そこで,Gにおける「力のモーメントが釣り合う」の条件は,つぎのようになります: 
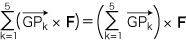
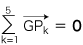
そこで,平板上に任意に x-y直交座標系を導入して,G(x, y),Pn(xn, yn) (n=1, 2, 3, 4, 5) とすれば,上の条件は,つぎのようになります: 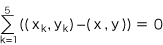
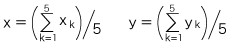
ここで,もとの正方形をつぎのように細分してみます: 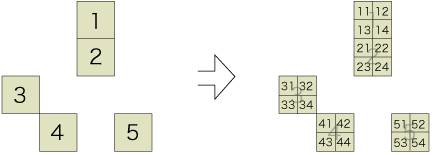
このとき,G(x, y) を求める式がつぎのように変わります: 
細分は重心の意味を変えませんから,この2通りの式は同値と見るべきです。 では,どうしたら同値に見えるでしょう? ここで,正方形の面積を考えに入れます。 左辺の正方形の面積 (数値) をΔとすると,つぎのようになります: 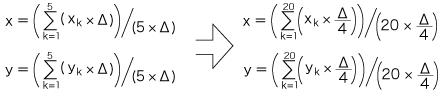
そして,両辺の式は,つぎの解釈で同値になります: 
|