そして,「黄金比」が,「フィボナッチ数」の出自である。 (  「フィボナッチ数の意味 (出自)」) 「フィボナッチ数の意味 (出自)」)
一方,「フィボナッチ数」は,独立に定義/定立することができる。 通常見る「フィボナッチ数」のテクストは,この構成をとる。 そしてこの場合は,「フィボナッチ数の比の極限」として「黄金比」を導くことになる。 ここでは,この構成を確認しておく。 A. フィボナッチ数列
F1 = 1 Fn+2 = Fn + Fn+1 これより,つぎの数列が生成される:
B. フィボナッチ数列の図形的生成 |
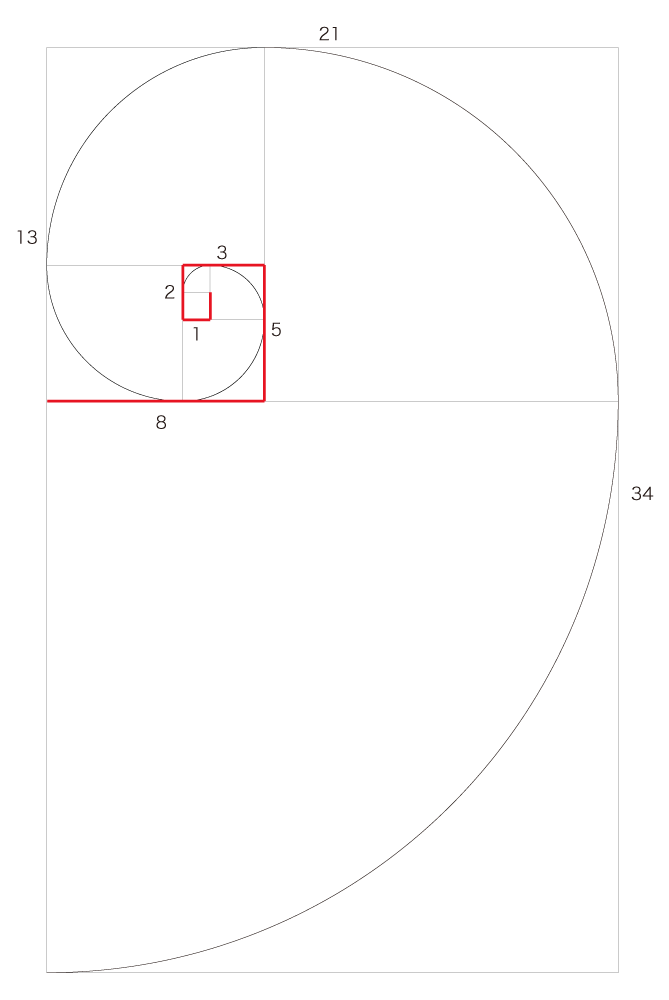
|
数は,正方形の辺の長さを表す;
赤線は,四半円の中心からつぎの四半円の中心への移動を表す |
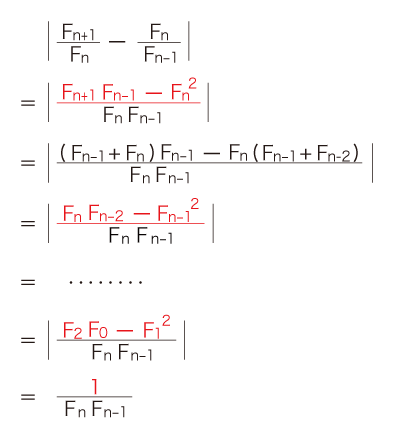
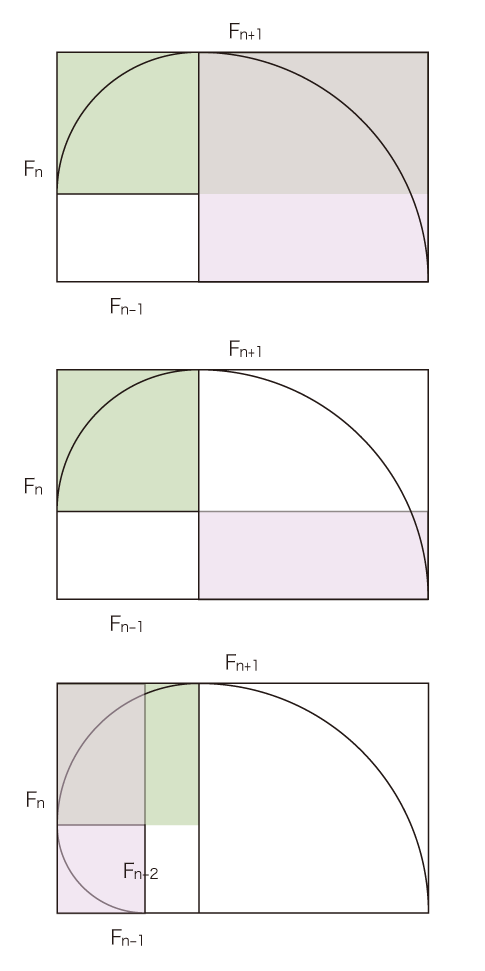
そして,1/(Fn Fn-1) は0に収束する。 D. 収束値φが,1 +φ = φ2 を満たすこと
そして,Fn + Fn+1 = Fn+2 だから,1 +φ = φ2。 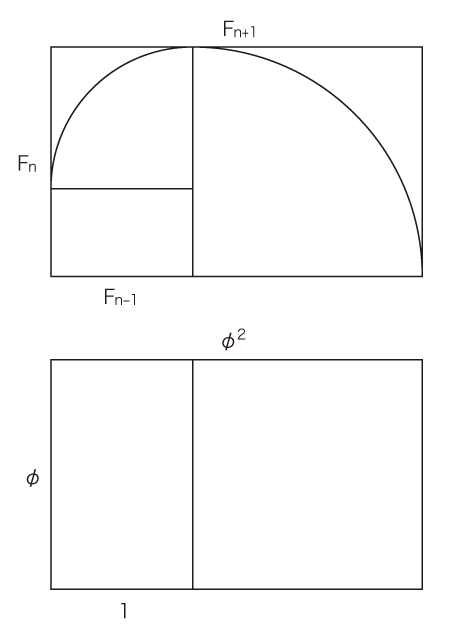
|