実際,古代ギリシアの数学は,「整数比」を中心的な主題の一つにするものであって,整数比を求めるアルゴリズムの「ユークリッドの互除法」をつくっていた。 そしてこのユークリッドの互除法で「無理数」をつくるときは,つぎの連分数で表される数が,「いの一番」のものになる: 
本テクストは,「黄金比」を「最もシンプルな無限互除を現す数」のストーリーで解説しようとするものである。 このとき,黄金比の連分数を数列に表現し直して,各項を計算すれば,「フィボナッチ数」が現れてくる。 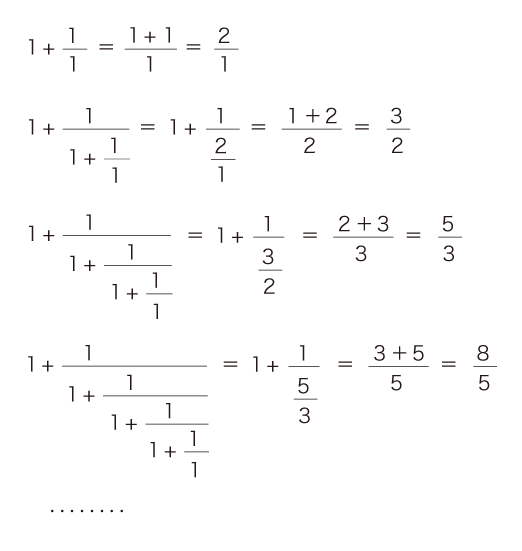
「フィボナッチ数」は,「イタリアの数学者フィボナッチの名にちなんで」となっているが,「黄金比」を本質的に構成するものであって,「黄金比」を主題化した古代ギリシア数学者の押さえるところとならなかったはずはない。 ところで,「黄金比」は,生物の形態形成学の方で,主題になる。 そしてこのときは,「フィボナッチ数──黄金角」が主題の趣きになる。 即ち,生物の形態形成にフィボナッチ数が見出されることに対し,これの理を形態形成学的に明らかにしようとして,「フィボナッチ数──黄金角」の論に進む。 わたしは生物形態形成学の方はまったくの素人だが,その中から聞こえてくる「フィボナッチ数──黄金角」の論には興味が引かれる。 実際,本テクストは,この興味が作成のもとになった。 ──特に,「全ての植物をフィボナッチの呪いから救い出す」(近藤滋) に触発されたものである。 |