Japanese
Conditions of Congruency for
1-Dimensional Plane Simplicial Complex
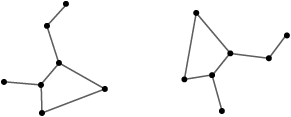
- 二つの1次元平面単体複体A,Bは,つぎの条件を満たすとき合同です:
Aの頂点全体の集合とBの頂点全体の集合の間の1対1対応 f で,つぎの条件を満たすものが存在する:
- Aの頂点 P と Q が辺を張るとき,しかもそのときに限り f(P) と f(Q) も辺を張る
- Aの頂点 P と Q が辺を張るとき,d(P, Q) = d(f(P), f(Q))
- Aの頂点 P,Q,R において,P と Q が辺を張り,Q と R が辺を張るとき,∠PQR = ∠f(P)f(Q)f(R)
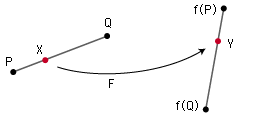
- 実際,この条件が満たされているとき,f はAとBの間の等長写像Fにつぎのような具合に拡張できます:
Aの頂点 P, Q と辺 PQ の上の点 X において v(P, X) = v(P, Q) x t であるとき,v(f(P), Y) =v(f(P), f(Q)) x t を満たす Y を,F(X) と定義する。
- 図形間の「点の対応」の問題が「頂点の対応」の問題に還元されてしまうのは,頂点の対応が辺および角の対応を決定してしまうからです。
頂点のどの重ね合わせに対しても全体が重ならなければ,もともと全体は重ならない(合同でない)というわけです。


