「直方体の切断面」の構成は，以下に示すものがシンプルである。
- つぎのものを考える：
- 平行２平面の組 P1 ＝ ( P11, P12 )
- P1 と直交する平行２平面の組 P2 ＝ ( P21, P22 )
- P1 と P2 は，横断面が長方形の筒の形Ｔをつくる。
- 平面Ｑを考える。
ＱとＴの位置関係を，つぎの２通りに分ける：
- 以下，Ａの場合だけを考えるとする。
- ＱとＴの交わりを，Ｑ′ とする。
Ｑ′ は平行四辺形。
そして，これをつぎの２通りに分ける：
Ａ-1. Ｑ′ は，長方形でない
Ａ-2. Ｑ′ は，長方形
- 以下，Ａ-1 の場合だけを考えるとする。
- Ｔと直交する平行２平面の組 P3 ＝ ( P31, P32 ) を考える。
Ｑ′ とP3 の交わりをＳとする。
このＳが，「直方体の切断面」になる。
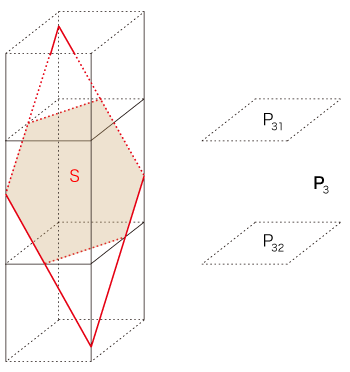（図は，わかりやすいように，Sの内部を着色）
- P31, P32 の位置関係により，Ｓは，三角形，四角形，五角形，六角形の形をとる。
- 五角形Ｓには，平行な２辺がある。よって，Ｓが正五角形になることはない。
ここでは，場合 A-2 と B を省略したが，これは考えなくてよいということではない。
場合分けが複雑になるので，省略しただけである。
練習： 省略した A-2 と B を，埋めよ。
|
