Up ベクトルの「行列」とテンソルの「行列」の比較 作成: 2018-02-25
更新: 2018-02-25

    学習者が悩む「テンソルと行列の違い」は，正しくはつぎの主題である：
      「ベクトルの行列とテンソルの行列の比較」


    先ず，「行列」は，「行列計算」を文脈にするものである。
    「行列」の格好をしていても，計算しないものは「行列」ではない。

    行配列・列配列は，１行行列・１列行列として計算にのせるとき，「行列」である。

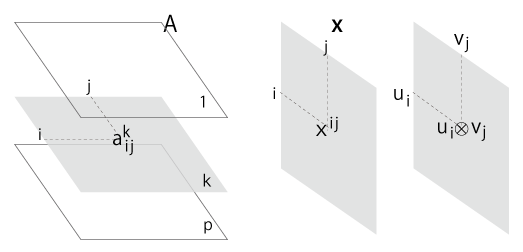
    「行列」は，平方構造である。
    平方構造に対しては，立方構造を考えることができる。
    立方構造は，これを「３次元」構造ととらえることで，任意次元に拡張できる──図には描けないが。
    「行列」をこのように次元拡張したものを，「超行列」と呼んでおく。

    以上の留保のもとに，ベクトルの「行列」は，つぎのものである：
    1. 線型空間 \( V \) の基底を構成するベクトルを，配列したもの :
        \( ( {\bf e}_1, \cdots, {\bf e}_n ) \)
    2. 基底 \( ( {\bf e}_i ) \) に対するベクトル \( {\bf x} \in V \) の座標を，配列したもの:
        \( ( x^1, \cdots, x^n ) \)
    3. ２つの線型空間 \( U,\, V\) それぞれの基底を固定したときの，線型写像 \( f : U \to V \) の表現行列：
      \[ \left( \begin{array}{ccc} a^1_1 & \cdots & a^1_n \\ & \cdots & \\ a^m_1 & \cdots & a^m_n \\ \end{array} \right) \]
    4. 線型空間 \( V \) の基底変換行列
    5. 基底変換行列に対する「座標変換行列」の読み換え

    そして，テンソルの「行列」は，つぎのものである：
    1. テンソル積 \( V_1 \otimes \cdots, \otimes V_n \) の各 \(V_i\) に伴う「行列」 (上述の「行列」)
    2. \( V_1 \otimes \cdots, \otimes V_n \) の基底 \( ( {\bf v}_1 \otimes \cdots \otimes {\bf v}_n ) \) を配列したもの (超行列)
    3. この基底に対する \( {\bf x} \in V_1 \otimes \cdots, \otimes V_n \) の座標を配列したもの (超行列)
    4. ２つのテンソル積それぞれの基底を固定したときの，両テンソル積間の線型写像の表現超行列
    5. テンソル積の基底変換超行列
    6. 基底変換超行列に対する「座標変換超行列」の読み換え