行列ないし高次表形式を「テンソル」と呼ぶ慣習──これが最も素朴に現れている例に,人工知能の知識表現手法「テンソル」がある。
類概念 (カテゴリー) を,集合に表す。
二つの集合
\[
A = \{ a_1, \cdots, a_m \} \\
B = \{ b_1, \cdots, b_n \}
\]
に対し,\( a_i \in A \) と \( b_j \in B \) の関係の強さを,\( r_{ij} \) で表す。
そして,行列
\[
\left(
\begin{array}{ccc}
r_{11} & \cdots & r_{1n} \\
& \cdots & \\
r_{m1} & \cdots & r_{mn} \\
\end{array}
\right)
\]
を,AとBの関係概念とする。
この関係概念は2次元であるが,つぎに次元を増やしていく。
即ち,新たな類概念を集合
\[
C = \{ c_1, \cdots, c_p \}
\]
として導入し, 「\( c_k \in C \) における \( a_i \in A \) と \( b_j \in B \) の関係」という考え方をする。
この関係は,\( r_{(ij),k} \) の表現になり,結局 \( r_{ijk} \) の表現になる。
そしてこれは,3次元の表をつくったことになる:
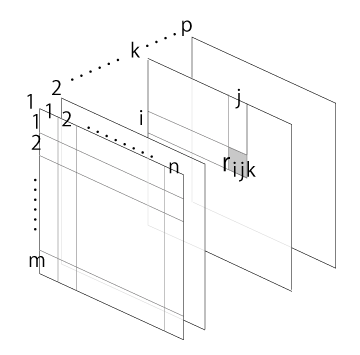
このやり方を繰り返すことで,高次元の関係概念をつくっていくことができる。
そして,この関係概念の表現は,高次元表である。
人工知能研究では,この形式を「テンソル」と呼んでいる。
「次元を増やす」の意味は,「概念を複雑にする」である。
人にとってふつうである概念は,分析するとひじょうに複雑なものになる。
人工知能研究は,この複雑のシミュレーションを課題にする。
そして,アプローチの一つが,「概念を<高次元表>に表現」──「テンソル」──というわけである。
|
