Up 面積計算 作成: 2018-01-23
更新: 2018-02-20

    長方形の面積は，つぎの可換図式の中の同型写像 \(\bar{\phi}\) によって，タテ\(\otimes\)ヨコと同一視されるものとなった：



    ところで，長方形の面積は，タテの長さの数値とヨコの長さの数値の積で計算される。
    即ち，長さの単位 \(\bf L\) と面積の単位 \(\bf S\) を
      \(\bf S\) ＝ 辺の長さが \(\bf L\) の正方形の面積
    の関係になるように択ったとき，
      タテの長さ　： \(\xi\,{\bf L}\)
      ヨコの長さ　： \(\eta\,{\bf L}\)
      長方形の面積： \(\zeta\,{\bf S}\)
    の間に，つぎの関係が成り立つ：
      \[ \xi \,\times\, \eta = \zeta \]

    小学数学だと，長さの単位「\(cm\)」に対しては面積の単位「\(cm^2\)」(\(cm\) 四方の正方形の面積) を暗黙に択り，長さの単位「\(m\)」に対しては面積の単位「\(m^2\)」(\(m\) 四方の正方形の面積) を暗黙に択るというふうにして，この数値計算を指導する：
      教師：「タテ \(2 cm\), ヨコ \(3 cm\) の長方形の面積は？」
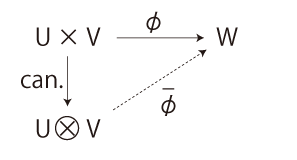
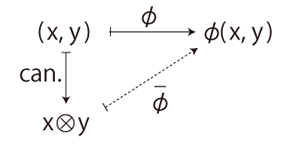
      生徒：「\(2 \times 3 = 6\)」
      　　　「だから，\(6 cm^2\)」


    数学の「×」は数の積の記号であるから，「\(2 cm \times 3 cm = 6 cm^2\)」と書いたら間違いである。
    しかし，このことを知らずに「\(2 cm \times 3 cm = 6 cm^2\)」とやってしまう者の方が，むしろありふれている。
    彼らにその間違いを説明することは，難しい。
    「テンソル積」を教えねばならないからである。

    「タテ \(2 cm\), ヨコ \(3 cm\) の長方形の面積は？」の計算は，
      \[ 2 {\bf cm} \otimes 3 {\bf cm} = ( 2 \times 3 ) ( {\bf cm} \otimes {\bf cm}) \]
    となる。
    要点は，二つの「積」が現れるということである──「\(\times\)」と「\(\otimes\)」。

    小学数学で「\(\times\)」と区別しつつ「\(\otimes\)」を教えることは，不可能である。
    そこで，小学数学は量計算をつぎのように指導しているわけである：
      《数値の積を計算し，その結果に単位をつける》