これは,対応をすべて示すものである。 振幅と周期が一定の波の場合,これの表現は対応をすべて示す形である必要はない。 即ち,振幅と周期と初期位相を示せばよい。 「フェーザ表示」はこれである。 振幅 \(V\), 角周波数 \(\omega\) の波を
と表す。ここで、\(\theta\) は初期位相。
ここで、
\( \dot{V} \) の導入の意味は,「\( v(t) \) の簡便な表現」の導入である: |
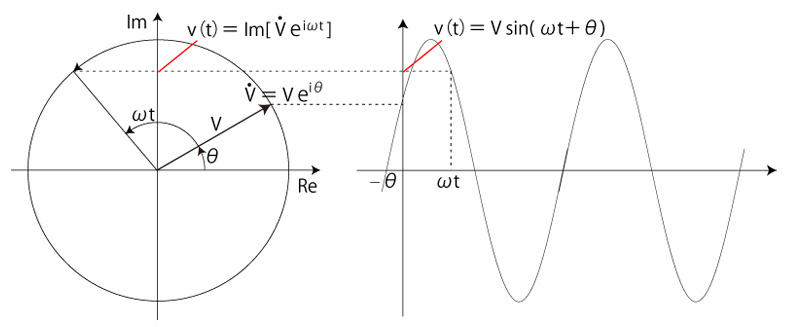
なお,\( v(t) \) を
|
| Up | フェーザ表示 | 作成: 2023-11-19 更新: 2023-11-19 |
これは,対応をすべて示すものである。 振幅と周期が一定の波の場合,これの表現は対応をすべて示す形である必要はない。 即ち,振幅と周期と初期位相を示せばよい。 「フェーザ表示」はこれである。 振幅 \(V\), 角周波数 \(\omega\) の波を
と表す。ここで、\(\theta\) は初期位相。
ここで、
\( \dot{V} \) の導入の意味は,「\( v(t) \) の簡便な表現」の導入である: |

なお,\( v(t) \) を

|