Up 分数の場合 作成: 2007-05-03
更新: 2007-05-04

    分数の求積公式は，正負の数や複素数の場合と比べてずっと複雑です。 したがってこのテキストでは，これを正負の数，複素数の後にもってきました。


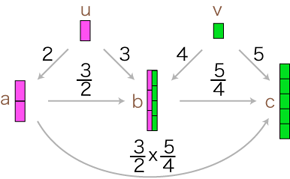
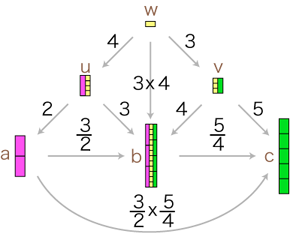
    さて，数の積は，倍の合成として定められます。 そこで分数の場合，つぎのようになります (図の中の倍は，長方形のタテの長さに関する倍)：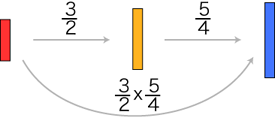


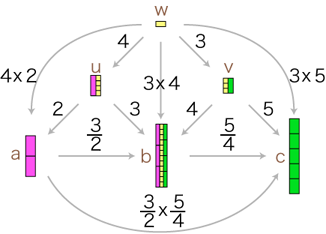
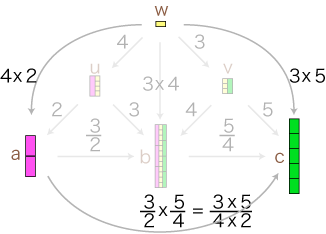
    この関係が成り立つようにするには，分数の積をどのように定めたらよいでしょう？
    先ずは，「3/2 × 5/4」が表す分数を求めてみます。

    1. 分数 3/2， 4/3 の意味により，下図の条件を満たす量 u, v がとれる。


    2. u の3 倍とv の4 倍が同じであることから，下図の条件を満たす量 w がとれる。


    3. a は w の (4 × 2) 倍，c は w の (3 × 5) 倍。
      すなわち，a と c は，w によって (4 × 2)：(3 × 5) の比になっている。


    4. よって，a に対する c の比は， (3 × 5)/(4 × 2)。



    この例から類推して，求積の公式がつぎのようになることがわかります：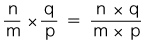

    通分
    量wは，「ｕ,vに共通の分割を求める」という方針で求めています。
    wを得て，このwから 比 3/2 : ａ→ｂ，5/4 : ｂ→ｃ を見るとき，２つの比はそれぞれ (４×3)/(４×2)，(３×5)/(３×4) になっています。
    特に，(3/2)×(5/4) は，(４×3)/(４×2)×(３×5)/(３×4) になります。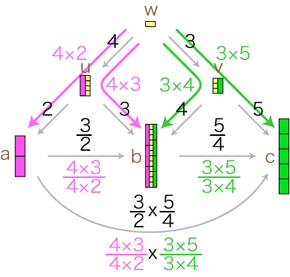
    これは何を意味しているでしょう？
    「ｕ,vに共通の分割を求める」は，「3/2 の分子と，5/4 の分母を通分する」に対応しているということです。
    つまり，つぎの形をつくっているわけです：
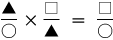
    この形の積の場合，求積公式はつぎのようになります──これが，分数の積の基本形（分数の和における「同分母分数の和」に対応するもの) ということになります：
    以下が，この求積公式の理由です：