「時刻の表現」から「位・量・数」の形式を導いてみます。
ゴールは,つぎの形式です:
(
時刻
,
+
,
(
時間
,
+
)
,
x
,
(
数,
+
,
x
)
)
- 時刻の表現では,時刻,時間,数がつぎのように互いに関係しています:
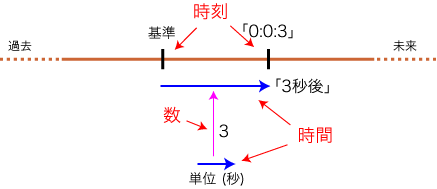
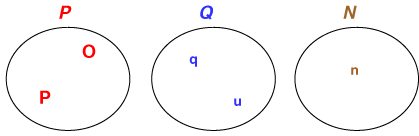
この絵では,「時刻 (位)」,「時間 (量)」,「数」という3つの異なる存在が想定されています。そこで,「時刻」の集合,「時間」の集合,「数」の集合を考える(想像する)ことにします。
- 集合「時刻」「時間」「数」は,「作用」という関係でつながっています。すなわち,
- ひとつの時刻に対しひとつの時間は「ずらし」の作用をする
- ひとつの時間に対しひとつの数は「倍」の作用をする
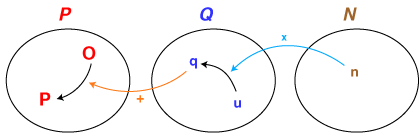
- 「時間a,bの和」として,わたしたちは集合「時間」の中では加法を考えています。
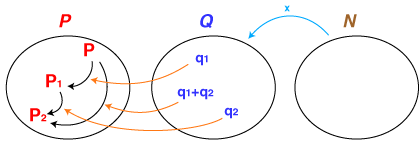
- 2倍と3倍の和は(2+3)倍,2倍して3倍すると(2×3)倍,‥‥ というように,わたしたちは「数」の中では加法と乗法を考えています。
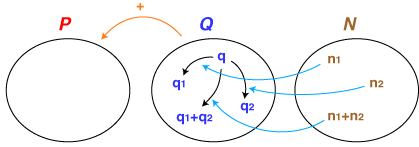
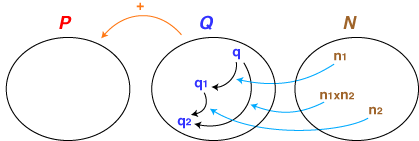
- 結局,「時刻・時間」の形式化として,つぎのものが得られました:
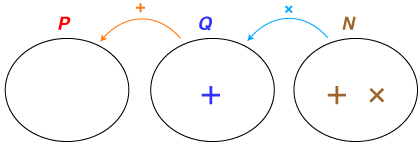
(
時刻
,
+
,
(
時間
,
+
)
,
x
,
(
数,
+
,
x
)
)







