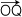 ( | ( |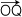 | = 1 ) を回転軸とする θ 回転 (0<θ<π) で,A が B に移るとします。 | = 1 ) を回転軸とする θ 回転 (0<θ<π) で,A が B に移るとします。
また,A の回転面と 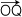 の交点を P とします。 の交点を P とします。
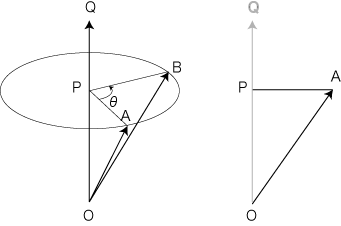
| 註 : |
回転の正方向は,つぎのように定義される:
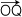 の向きと対面して左回り(反時計回り) が正。 の向きと対面して左回り(反時計回り) が正。
(言い換えると,回転して右ネジが進む方向が 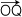 の向きになるときが,正。) の向きになるときが,正。)
|
Q の座標 (qx, qy, qz),A の座標 (ax, ay, az),角度θ に対する B の座標 (bx, by, bz) は,以下のようにして求めることができます:
- P を定める条件:
この条件は,以下を含意する:
- k
=
qx
ax
+
qy
ay
+
qz
az
- |
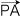 | = r とするとき, | = r とするとき,
r2
= |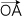 |2
ー | |2
ー |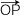 |2
= ax2 + ay2 + az2
ー k2 |2
= ax2 + ay2 + az2
ー k2
- B を定める条件:
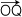 ・ ・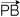 = 0 = 0
|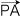 | = | | = |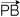 | |
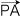 ・ ・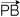 = |
= |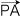 | | | |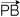 | cos θ
= r2 cos θ | cos θ
= r2 cos θ
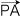 × × 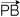 = t
= t 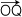 ( t > 0 )(註) ( t > 0 )(註)
この条件は,以下を含意する:
- k
=
qx
bx
+
qy
by
+
qz
bz
- |
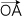 | = | | = |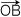 | |
- ax bx
+ ay by
+ az bz
= r2 cos θ
- t
= |
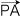 × × 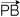 |
= r2 sin θ |
= r2 sin θ
- 以上の条件を bx, by, bz に関する方程式として,計算する。
結果は,つぎのようになります:
| bx = |
(
cosθ
+
qx2
ー
qx2
cosθ
)
ax
+
(
qx
qy
ー
qx
qy
cosθ
ー
qz
sinθ
)
ay
+
(
qx
qz
ー
qx
qz
cosθ
+
qy
sinθ
)
az
|
| by = |
(
cosθ
+
qy2
ー
qy2
cosθ
)
ay
+
(
qy
qz
ー
qy
qz
cosθ
ー
qx
sinθ
)
az
+
(
qy
qx
ー
qy
qx
cosθ
+
qz
sinθ
)
ax
|
| bz = |
(
cosθ
+
qz2
ー
qz2
cosθ
)
az
+
(
qz
qx
ー
qz
qx
cosθ
ー
qy
sinθ
)
ax
+
(
qz
qy
ー
qz
qy
cosθ
+
qx
sinθ
)
ay
|
( 計算のプロセス) 計算のプロセス)
| 註 : |
ベクトル (x, y, z) と (X, Y, Z) に対する 外積 (x, y, z) × (X, Y, Z) は,つぎのベクトル:
- (x, y, z) と (X, Y, Z) が張る平面に垂直
- 向きは,これを回転軸にして (x, y, z) を (X, Y, Z) に重ねるときの右ねじの進む方向
- 大きさは,(x, y, z) と (X, Y, Z) のなす角θに対し,|(x, y, z)| |(X, Y, Z)| sinθ
|
|
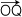 ( |
( |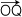 | = 1 ) を回転軸とする θ 回転 (0<θ<π) で,A が B に移るとします。
| = 1 ) を回転軸とする θ 回転 (0<θ<π) で,A が B に移るとします。
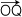 の交点を P とします。
の交点を P とします。

 計算のプロセス)
計算のプロセス)
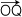 ( |
( |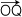 | = 1 ) を回転軸とする θ 回転 (0<θ<π) で,A が B に移るとします。
| = 1 ) を回転軸とする θ 回転 (0<θ<π) で,A が B に移るとします。
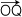 の交点を P とします。
の交点を P とします。

 計算のプロセス)
計算のプロセス)