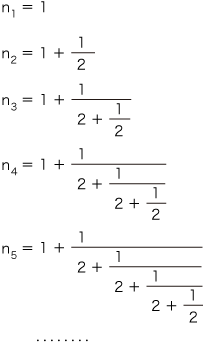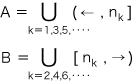以下,無理数 √2 に対応する Cauchy 列と Dedekind 切断を示します。 正方形の辺の長さと対角線の長さに対するユークリッドの互除法は,延々と続いて終わりません。そしてこれは,√2 が無理数であることの直接証明になっています。(  √2 が無理数であることの証明) √2 が無理数であることの証明)
いま,正方形の辺と対角線の長さ,互除法の中で現れる余りの線分の長さに,つぎのように記号をあてます: 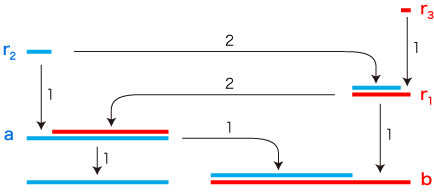 このとき,つぎの関係が成り立っています: 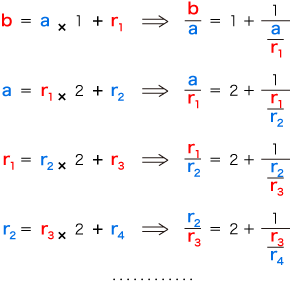
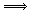 の左辺は量の等式,右辺は数の等式。 の左辺は量の等式,右辺は数の等式。
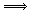 の右辺の「量/量」は,この2量の比になっている数。 の右辺の「量/量」は,この2量の比になっている数。
そしてこれから,つぎが導かれます: 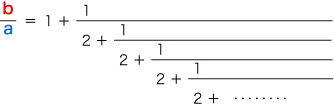 |