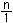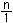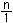4.1.5 NRの中へのNの埋め込み
算数科では,分数と自然数の使用場面を援用することで,分数に自然数を直接外挿する。しかしこれは本来,“NRの中へのNの埋め込み”のように主題化されねばならない主題である。
NR が量の係数の系と意味づけられているとき,“量のn回の累加”を量に対するn∈Nの倍作用と考えれば,n∈Nに関するn倍とn/1倍は同値である。このことを見て,“NR の中へのNの埋め込み”をつぎのような形で導入する。
写像i:N─→NR を
| i(n)= | 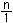 | (n∈N)
|
で定義するとき,iは1対1で,
i(m+n)=i(m)+i(n)
i(m×n)=i(m)×i(n)
が成り立つ。そこでこのiによって,(N,+,×)を(NR,+,×)の部分(i(N),+,×)と同一視できることになる。言い換えると,iによって,(N,+,×)は(NR,+,×)に埋め込まれる。またこの意味で,NRはNの拡張である。
n ∈Nの表記を,i(n)∈NR の表記に流用する。
このとき,1∈NはNR の単位元。また,n∈Nに対し
| n= | 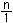
|
であり,かつ 1/n が×に関する n の逆元 n-1 になる。