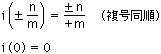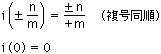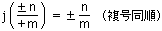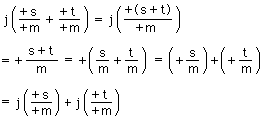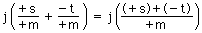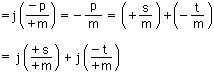4.3.1 (NR)Dと(ND)Rの同型性(=NRD)
学校数学では,Nの要素m,nに対する (NR)D の要素±(n/m) と (ND)R の要素 (±n)/(+m) の同一視を暗黙に導入する。これは本来,“(NR)Dと(ND)Rの同型”という主題になる。
実際,
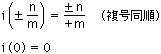
で定義される写像i:(NR)D ─→(ND)R は,((NR)D,+,×)の((ND)R,+,×)の上への同型になっている(註)。
特に,(NR,+,×)からの((NR)D,+,×)の導出と,(ND,+,×)からの((ND)R,+,×)の導出では,実質的に同じ対象がつくられる。
(註) (1) 先ず,

であるので,写像j:(ND)R ─→(NR)D が
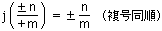
で定義でき,かつこれはiの逆写像になる。
(2) あとは,
j(x+y)=j(x)+j(y)
j(x×y)=j(x)×j(y)
が確かめられればよい。
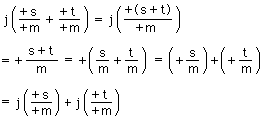
また,
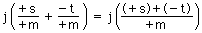
において例えばs+p=tならば,s/m+p/m=t/mであるから,上式はつぎのように続く:
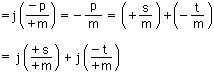
残りについては,省略する。