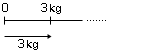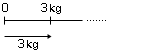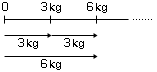7.2.4 量直線/量平面,数直線,複素平面
数の系N=(N,+,×) ないし量の系Q=((Q,+),N,×) から導出される位の系S=(S,Q,+) が直線/平面をそれの絵としてもてるとき,この絵をN,Qの絵とすることができる(註)。
“数直線”は,この意味での〈実数の系の絵〉であり,直接的には位としての実数の絵である。実数の系に埋め込むことができる数の系に対しては,〈埋め込み〉に対応して,数直線の中にこれを表示することができる。
同様に,“複素平面”は複素数の系の絵であり,直接的には位としての複素数の絵である。
なお,現行の“数直線”の扱いには問題がある。“数直線”は上に述べたように“位としての数”の絵であり,“数”の直接のイメージではない。(数直線を数のイメージとして指導するのは,間違いである。)特に,それは“数”に対する誤解を招きやすい。したがって,数直線の指導は本来,これの構成規則と使用の構造をしっかり扱うものでなければならないのである。数直線の意義は,“数のイメージ”ではなく,“位の系の普遍対象”である。このような意義において問題解決に有効な道具となる。問題解決での効用のために誤解を招きやすい素材を敢えて導入しているということを,忘れてはならない。
(註) 例えば重さが,1次元の量の系として
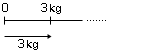
のように直線表示される。──ここで,直線上の点である 3kg はSの元として,矢線の 3kg はQの元として,それぞれ意味づけられる。
このとき,例えば“3kg の 3kg増で 6kg”の図式は,
3kg+3kg=(0+3kg)+3kg = 0+(3kg+3kg)=0+6kg=6kg
と読むことによって,
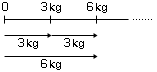
のようになる。