はじめに,「数・量」の算法を思い起こしてして下さい。
OKであれば,以下へ進んで下さい。
- ここでは,「比例関係」と呼ばれる2量の間の対応関係の一つ(基本的でありそしてひじょうに重要な2量間関係)を主題にします。
- 比例関係は,算数科では,
「一方が2倍,3倍,‥‥ になるとき,もう一方も2倍,3倍,‥‥ になる」
の言い回しで導入されます。
例えば,「(一定の)速さ」は,「時間」と「距離」の間の比例関係と解釈されます:
「経過時間が2倍,3倍,‥‥ になれば移動距離も2倍,3倍,‥‥」
- ここで,上の定義(ことばによる定義)の言い換えになる二つの形を,紹介します。──図による定義と式による定義です。
わかりやすいように,一般的な形で定義を示すのではなく,速さ「2m/秒」を使うことにします。
速さ「2m/秒」には,「時間が2倍,3倍,‥‥ になれば距離も2倍,3倍,‥‥」が含まれています。──実際,「5秒のときは10m」と答えるとき,この条件を使っていることになります。(「秒の5倍には,秒に対応している2m の5倍が応ずる」)
ここで,「集合」の考え (フィクション) を受け入れてください。──時間の集合 (すべての時間を要素とする集合) と距離の集合 (すべての距離を要素とする集合) 。
このとき,「2m/秒」における「時間が2倍,3倍,‥‥ になれば距離も2倍,3倍,‥‥」は,つぎのように言い換えられます:
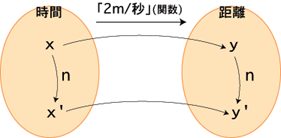
(n = 1, 2, 3, ‥‥)
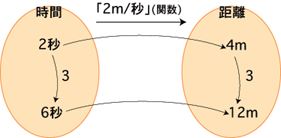
つぎに,関数「2m/秒」を f で表して,上の図を式に置き換えてみましょう。つぎにようになります:
f(x x n) = f(x) x n
(ただし,x は倍作用の記号)
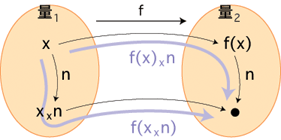
最後の図は,敢えて一般的な形に書きました。
- 改めて確認: 比例関係の定義の3形態
(見かけは違っても,定義していることは同じ!) :
「一方が2倍,3倍,‥‥ になるとき,
もう一方も2倍,3倍,‥‥ になる」
f(x x n) = f(x) x n
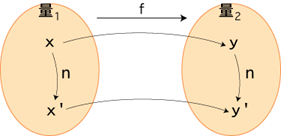
- 以上の表現を十分理解し自ら使えるようにしてください。
|







