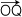 ( | ( |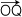 | = 1 ) を回転軸とする θ 回転 (0<θ<π) は,3次元ベクトル空間の変換を導きます。 | = 1 ) を回転軸とする θ 回転 (0<θ<π) は,3次元ベクトル空間の変換を導きます。
すなわち,Q の座標を (qx, qy, qz) とするとき,この変換は (ax, ay, az) につぎのように定まる (bx, by, bz) を対応させるものになります (  回転の計算): 回転の計算):
また,「倍」をこの回転と合わせることができます。 しかし,この「回転・倍」の作用は,3次元ベクトルを「量」とする「2量の比」としては使えません。 なぜなら,任意の (ax, ay, az), (bx, by, bz) に対し, (ax, ay, az) を (bx, by, bz) に移す「回転・倍」が一意に決まらないからです。 ──実際,可能な回転がいくつもあります。(  「回転・倍」は「2量の比」の表現に使えない) 「回転・倍」は「2量の比」の表現に使えない)
この「回転がいくつもある」という問題に対し,つぎのように考えてみます:
このように考えてみようというのは,つぎの可能性が考えられるからです:
すなわち,ここに「四元数」の登場となって,「回転」は (ar, ax, ay, az) に対する ( θ, qx, qy, qz) のつぎの作用「x 」になります:
br +bx i +by j +bz k = ( cos(θ/2) + qx sin(θ/2) i + qy sin(θ/2) j + qz sin(θ/2) k ) × (ar + ay j + ay j + az k) × ( cos(ーθ/2) + qx sin(ーθ/2) i + qy sin(ーθ/2) j + qz sin(ーθ/2) k ) そしてこのとき, (0, ax, ay, az) には (0, bx, by, bz) が対応して,これは3次元ベクトル空間での回転になっています。 (  回転の計算に四元数が使える) 回転の計算に四元数が使える)
|