6.5.1 位の系
われわれはさらに,“量形式”,“量の系”の上位概念として“位(くらい)形式”,“位の系”の概念を導入することにしよう。
先ず,数の系(N,+,×)に対し,これの差の系 (ND,+,×) を導入する。NはNDの部分になる──Nの+が群算法であればNとNDは一致する。
つぎに,N0=N∪{0} とおいて,系:
(N0,((ND,+),(ND,+,×),×),+)
を位形式と定め,これと同型な系
(S,((Q,+),(ND,+,×),×),+)
を位の系と呼ぶ。──ここで,
- Sの要素の身分は“位”;
- Qの要素の身分は“変位”;
- 最後の項の+の身分は,“位に対する変位の作用"(註1)
のように読む。実際,X,Y∈Sに対しX+x=Yとなるx∈Q(これは一意的に存在する)を,Xに対するYの変位と呼び,
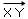 で表わす。
で表わす。
つぎのことが成り立つ(註2):
- Qには零元 0 が存在し,かつX∈Sに対し
X+0=X
- X∈Sとx,y∈Qに対し,
(X+x)+y=X+(x+y)
- X∈Sとx,y∈Qに対し,
X+x=X+y  x=y
x=y
Sには基準O(オー)が存在する──即ち,Sの要素Oでつぎの条件を満たすものが存在する(註3):
各X∈Sに対し,X=O+xとなるx∈Qが(一意的に)存在する.
(註1) N≠NDであれば,作用+はつねには定義されない。
(註2) (S,((Q,+),(ND,+,×),+,×),×),+) は (N0,((ND,+,×),+),(ND,+,×),+,×),×),+) と同型。一方,
- ND,+,×)には零元 0 が存在し,かつX∈N0に対し,X+0=X;
- X∈N0とx,y∈ND,+,×)に対し,(X+x)+y=X+(x+y);
- X∈N0とx,y∈ND,+,×)に対し,X+x=X+y
 x=y。
x=y。
(註3) (N0,((ND,+),(ND,+,×),×),+) と(S,((Q,+),(ND,+,×),×),+) の同型において,0∈N0 に対応するSの要素が所期のO。
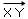
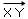
 x=y
x=y
 x=y。
x=y。