Up 和/加法の定義  

    一般に，数の和は，道具としてつぎのように使われるよう導入されています。すなわち

      数ｍ，ｎと量ｕ，ｑ，ｒが

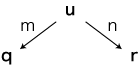
      の関係にあるとき，ｕに対するｑ＋ｒの比を「ｍ＋ｎ」で表す。


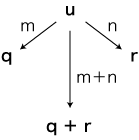
(注意： 量の「＋」と数の「＋」を区別すること)
      式で表すと：
ｕｘｍ ＋ ｕｘｎ ＝ ｕｘ (ｍ＋ｎ)

    特に，量の「＋」が，数の「＋」より先に導入されていることになります。
    「正負の数」の場合だと，「正逆２方向をもつ量」の「＋」が，「正負の数」の「＋」より先に導入されていることになるわけです。


    さて，数の「＋」のこの用い方を保証する「正負の数」の和は，どのように定義されるものになるでしょう？

    それはつぎのようになります。ただし，数ｎを「符号つきの自然数/分数」と見たときのその符号を sgn(ｎ)，自然数/分数を val(ｎ) で表すことにします。

  1. ｎ＋０＝０＋ｎ＝ｎ
  2. ｍ ＋ (ーｍ) ＝ ０

  3. ｍ，ｎ≠０に対し，

      (1) ｍとｎが同符号のとき，
        sgn(ｍ＋ｎ)＝sgn(ｎ)
        val(ｍ＋ｎ)＝val(ｍ)＋val(ｎ)

      (2) ｍとｎが異符号でval(ｍ)≦val(ｎ) なら
        sgn(ｍ＋ｎ)＝sgn(ｎ)
        val(ｍ＋ｎ)＝val(ｎ)−val(ｍ)



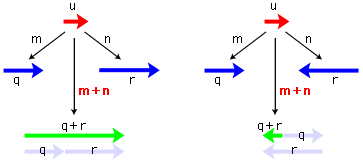
    一般に，数の加法は，数の和が定義されているときの関数：
（ｍ，ｎ） ｍ＋ｎ
（「２数にそれらの和を対応させる」）
    として定義されます。「正負の数」の場合もこれにしたがいます。