- わたしたちは個々に,「回転の大きさ」のイメージをもっています。
この個的なイメージをひとに共有されるものにしようとするとき,具体的な表現が問題になります。そしてそれは,「何かの回転の大きさ」として表現することになります。
- 数学では,「回転の大きさ」を「半直線のそれの端点を中心とした回転の大きさ」に帰着させます。
例えば,「一点を中心とした点の回転の大きさ」は,つぎのように「半直線のそれの端点を中心とした回転の大きさ」に帰着させます:
- 点Mを中心とした点Xの回転で,Xが点Yに移ったとします。
- この回転の大きさを,半直線MXから半直線MYへのMを中心とした回転の大きさと見なします。
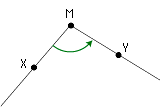
- このように考えた「回転の大きさ」は, 正逆2方向をもつ量になります。──特に,二つの回転の間の比 (倍) は「正負の数」で表現されます:
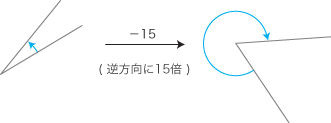
- 回転の向きに正負を定めるときは,時計の反対回りを正,それの逆を負とします。
- なお,あたりまえですが,回転の結果からもとの回転を知ることはできません。ある回転の結果と,その回転に 1, 2, 3, ‥‥ 回転を加えた回転の結果は同じだからです。
プロセスは結果に現れませんから,回転はプロセスとして記述することが必要になります。
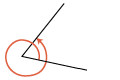
- 回転の大きさは,「n回転とプラスどれだけ」の「どれだけ」で,類別することができます。(例えば,30度,(30+360×1) 度,(30+360×2) 度, ‥‥ は同類。)
|





