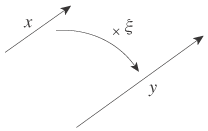
日常語の“変位”については,
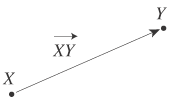
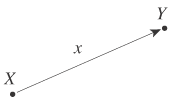
いま,変位全体の集合Dを仮構し,上の要件 (b) を,
 X+x; X+x;
E×D ─→ E
日常語の“変位”については,さらに,
 は実数全体の集合を表わす)。 は実数全体の集合を表わす)。
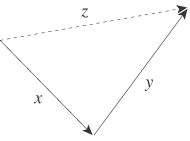
日常語の“変位”では,変位の合成は結合法則,交換法則が成立することになっており,また各変位に対しそれを解消する変位が存在することになっています。 変位の解消は変位の合成であるから,算法+を導入した手前,その結果もまた一つの変位であると約束しておいた方が形式操作上都合がよい。そこで,零を導入します。零は,“任意の変位xに対し,xとこれの合成はx”という条件で特徴づけられます。 以上のことからわたしたちは,Dにおける(内)算法+をつぎの条件を満たすものとして定式化する: x+y=y+x
実数のここでの意味は,変位に対する倍です。 “倍”については,和と合成を考えることができます。この和,合成はそれぞれ,実数の(内)算法の+,×と一致します。しかも,わたしたちは《実数=倍》の意味において
 *= *= \{0}(註1))ということにし,また+と×の間には分配法則 \{0}(註1))ということにし,また+と×の間には分配法則
 の構造の通常の捉え方:“システム の構造の通常の捉え方:“システム
 ,+,×) ,+,×)
 はもともと倍の構造の定式化なのであるから,これはアタリマエです。 はもともと倍の構造の定式化なのであるから,これはアタリマエです。
さて,Dの要素に対する実数の作用×については,わたしたちは (x+y)×ξ=x×ξ+y×ξ x×(ξ+η)=x×ξ+x×η
 についてのこれまでの条件にこの条件を加えるとき,わたしたちはシステム についてのこれまでの条件にこの条件を加えるとき,わたしたちはシステム
 ,+,×),×) ,+,×),×)
 ,+,×) 上の線型空間) として定式化したことになります。 ,+,×) 上の線型空間) として定式化したことになります。
最後に,Eの要素に対するDの要素の作用 + についてわたしたちは
 ,+,×),×),+) ,+,×),×),+)
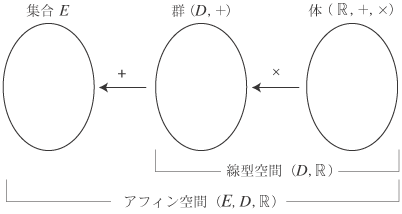
なお,誤解の恐れのないときには,表記 ((D,+),(  ,+,×),×),(E,((D,+),( ,+,×),×),(E,((D,+),( ,+,×),×),+) の代わりに,それぞれ表記(D, ,+,×),×),+) の代わりに,それぞれ表記(D, ),(E,D, ),(E,D, )を使っていくことにします。 )を使っていくことにします。
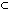 Zに対し,X\Yは{x Zに対し,X\Yは{x Z|x Z|x Xかつx Xかつx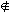 Y}のように定義される集合。 Y}のように定義される集合。
(註2) 記述の上では,アフィン空間Eがベクトル空間D込みで成立する概念であるのに対し,ベクトル空間Dはアフィン空間の概念を要しません。しかし,“現空間”の契機ということでは,EとDは同時です。 即ち,一方が他方から導かれるというのではなく,相互依存的な関係にある。──実際,ベクトルは二点(始点と終点)に対して考えられるのみです。 そして所在としての二点は,位置の違い(=変位(ベクトル)の存在)として現前している事態です。 |