Up スカラー場 作成: 2018-01-15
更新: 2018-01-15

    「地図帳に情報を書き込む」のところで，つぎのことを考えた：
      多様体 \(M\) の各点 \(\bf x\) にスカラー値 \(f(\bf x)\) を対応させる関数 \(f\) を立てる：
        \[ f : M \longrightarrow \mathbb{R} \]
      \(f(\bf x)\) を，地図帳の各ページ \(\phi\) に書き込む。

    書き込みは，つぎの図式を可換にする関数 \( F_{\phi} \) ── 即ち，\( F_{\phi} = f \circ \phi^{-1}\) ──として表現される：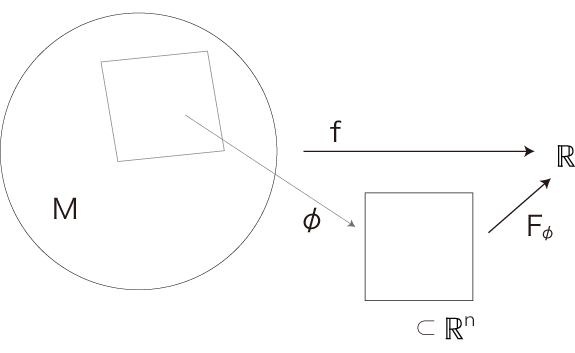

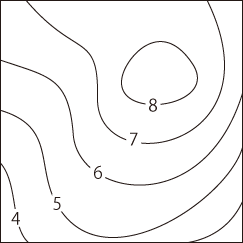
    \(f(\bf x)\) を地図帳の各ページ \(\phi\) に書き込むのは，地図帳を用いて \(f(\bf x)\) を解析するためである。
    実際，地図帳は，空間 \( M \) の解析のために導入されたのである。


    スカラー値関数 \( f \) から導かれる上の図式の構造を指して，「\( M \) は \(f\) によるスカラー場である」と謂う。

    スカラー場の地図の特徴は，「等高線」である。

      例えば \( F_{\phi}^{-1}(5) \) は，( \(f\) が連続の場合)「５度」の等高線である。