つぎを,デカルト座標の2つの基底とする:
\[
{\bf E} = \{ {\bf E}_1,\, \cdots,\, {\bf E}_n \}
\\{\bf E'} = \{ {\bf E'}_1,\, \cdots,\, {\bf E'}_n \}
\]
そして,これに対する座標を,それぞれ \(X^i,\, {X'}^i\) 座標と呼ぶ。
つぎを,それぞれ \(X^i,\, {X'}^i\) 座標に伴う曲線座標の基底──局所直線基底──とする:
\[
{\bf e} = \{ {\bf e}_1,\, \cdots,\, {\bf e}_n \}
\\{\bf e'} = \{ {\bf e'}_1,\, \cdots,\, {\bf e'}_n \}
\]
そして,これに対する座標を,それぞれ \(x^i,\, {x'}^i\) 座標と呼ぶ。
これらの間には,つぎの関係が成り立つ:
\[
( {\bf E'}_1\, \cdots\, {\bf E'}_n )
= ( {\bf E}_1\, \cdots\, {\bf E}_n )
\left(
\begin{array}{ccc}
\frac{\partial {X}^1}{\partial {X'}^1} & \cdots & \frac{\partial {X}^1}{\partial {X'}^n} \\
& \cdots & \\
\frac{\partial {X}^n}{\partial {X'}^1} & \cdots & \frac{\partial {X}^n}{\partial {X'}^n} \\
\end{array}
\right)
\\ \\
( {\bf e'}_1\, \cdots\, {\bf e'}_n )
=
( {\bf e}_1\, \cdots\, {\bf e}_n )
\left(
\begin{array}{ccc}
\frac{\partial {x}^1}{\partial {x'}^1}
& \cdots &
\frac{\partial {x}^1}{\partial {x'}^n} \\
& \cdots & \\
\frac{\partial {x}^n}{\partial {x'}^1}
& \cdots &
\frac{\partial {x}^n}{\partial {x'}^n} \\
\end{array}
\right)
\]
つぎは,\( \phi_P\) 上での ベクトル \(\bf A\) の平行移動 \( P \to P'\) を,\( \phi_P'\) から読み込んだものである。
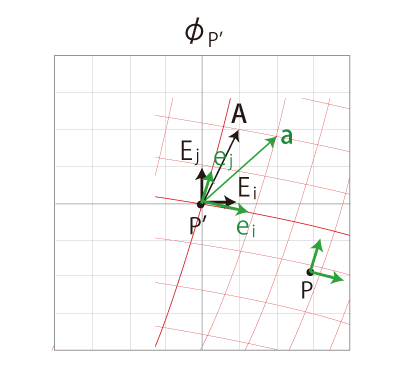
(図中の \(\bf A\) は, \(\phi_P\) での \(A\) を, そのデカルト座標を以て, \(\phi_P'\) で再現したもの)
またつぎは,デカルト座標の基底を変換したものである:
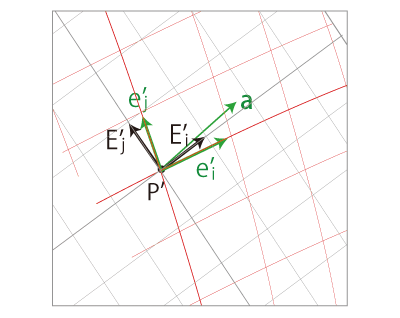
デカルト座標とこれに伴う曲線座標のそれぞれに対する \(\bf a\) の座標を,つぎのように定める:
| \(A_i = {\bf a} \cdot {\bf E}_i \) | :\({\bf E}\) に対する座標 |
| \(A'_1 = {\bf a} \cdot {\bf E'}_i \) | :\({\bf E'}\) に対する座標 |
| \(a_1 = {\bf a} \cdot {\bf e}_i \) | :\({\bf e}\) に対する座標 |
| \(a'_1 = {\bf a} \cdot {\bf e'}_i \) | :\({\bf e'}\) に対する座標 |
ここで,座標の表記が,添字が下付けになっている。
理由は,これらの座標が「基底変換と共変」と特徴づけられるものになるからである。
このことを,以下に示す。
(1) \({\bf E} \to {\bf E'}\) に対する \( A_i \to A'_i \)
このとき
\[
\begin{align*}
A'_i &= {\bf a} \cdot {\bf E'}_i
= {\bf a} \cdot \sum_j \frac{\partial {X}^i}{\partial {X'}^j}\, {\bf E}_j
= \sum_j \frac{\partial {X}^i}{\partial {X'}^j}\, {\bf a} \cdot {\bf E}_j
\\&= \sum_j \frac{\partial {X}^i}{\partial {X'}^j}\, A_j
\end{align*}
\]
即ち,\({\bf E} \to {\bf E'}\) :
\[
( {\bf E'}_1\, \cdots\, {\bf E'}_n )
= ( {\bf E}_1\, \cdots\, {\bf E}_n )
\left(
\begin{array}{ccc}
\frac{\partial {X}^1}{\partial {X'}^1} & \cdots & \frac{\partial {X}^1}{\partial {X'}^n} \\
& \cdots & \\
\frac{\partial {X}^n}{\partial {X'}^1} & \cdots & \frac{\partial {X}^n}{\partial {X'}^n} \\
\end{array}
\right)
\]
と \( A_i \to A'_i \) :
\[
( {A’}_1\, \cdots\, {A’}_n )
= ( A_1\, \cdots\, A_n )
\left(
\begin{array}{ccc}
\frac{\partial {X}^1}{\partial {X'}^1} & \cdots & \frac{\partial {X}^1}{\partial {X'}^n} \\
& \cdots & \\
\frac{\partial {X}^n}{\partial {X'}^1} & \cdots & \frac{\partial {X}^n}{\partial {X'}^n} \\
\end{array}
\right)
\]
が共変である。
(2) \({\bf E} \to {\bf E'}\) に対する \( a_i \to a'_i \)
\({\bf E} \to {\bf E'}\) には \({\bf e} \to {\bf e'}\) が随う。
そしてこのとき,
\[
\begin{align*}
a'_i &= {\bf a} \cdot {\bf e'}_i
= {\bf a} \cdot \sum_j \frac{\partial {x}^i}{\partial {x'}^j}\, {\bf e}_j
= \sum_j \frac{\partial {x}^i}{\partial {x'}^j}\, {\bf a} \cdot {\bf e}_j
\\&= \sum_j \frac{\partial {x}^i}{\partial {x'}^j}\, a_j
\end{align*}
\]
即ち, \({\bf e} \to {\bf e'}\)
\[
( {\bf e'}_1\, \cdots\, {\bf e'}_n )
= ( {\bf e}_1\, \cdots\, {\bf e}_n )
\left(
\begin{array}{ccc}
\frac{\partial {x}^1}{\partial {x'}^1} & \cdots & \frac{\partial {x}^1}{\partial {x'}^n} \\
& \cdots & \\
\frac{\partial {x}^n}{\partial {x'}^1} & \cdots & \frac{\partial {x}^n}{\partial {x'}^n} \\
\end{array}
\right)
\]
と \( a_i \to a'_i \) :
\[
( {a’}_1\, \cdots\, {a’}_n )
= ( a_1\, \cdots\, a_n )
\left(
\begin{array}{ccc}
\frac{\partial {x}^1}{\partial {x'}^1} & \cdots & \frac{\partial {x}^1}{\partial {x'}^n} \\
& \cdots & \\
\frac{\partial {x}^n}{\partial {x'}^1} & \cdots & \frac{\partial {x}^n}{\partial {x'}^n} \\
\end{array}
\right)
\]
が共変である。
|

