「曲線座標の地図」は,以下に述べる「地図 \( \phi_{P'}\) への地図 \( \phi_{P}\) の読み込み」である:
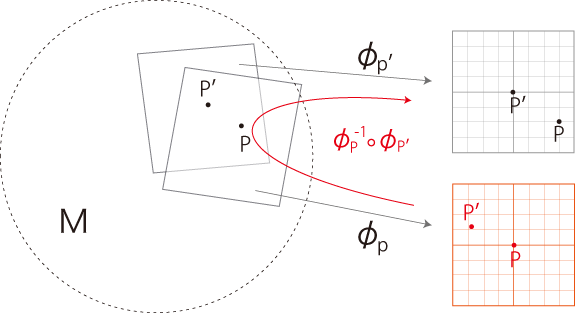
「読み込み」は,つぎの操作である:
- \(\phi_P\) での \(P'\) の座標を \( ({X}_0^i) \) とする。
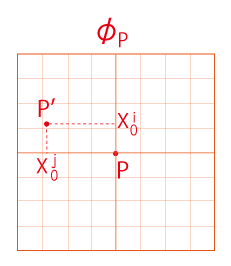
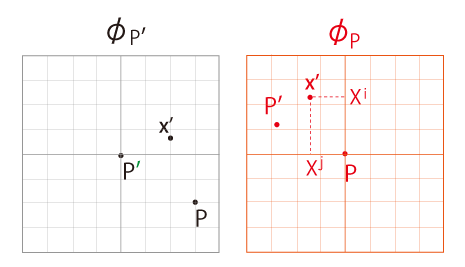
- \(\phi_P'\) 上の点 \( \bf x'\) で,\(\phi_P\) にも載っているものに対し,
\(\phi_P\) における \( \bf x'\) の座標が \( (X^i)\) であるとき,
\( ( x'^i ) = ({X}^i - {X}_0^i)\) を \( \bf x'\) の新座標とする。
デカルト座標のメッシュに対応する新座標のメッシュは,下図の赤色のメッシュのようになる:
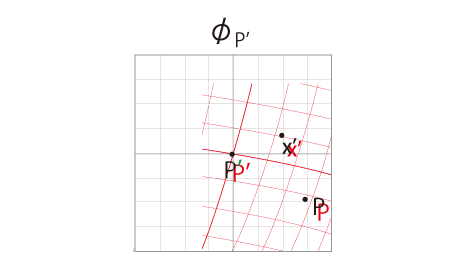
考え方:
\(\phi_P\) の原点を \(P'\) に移動
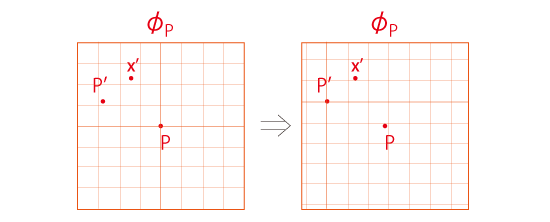
\(\phi_P' \) に \(\phi_P\) を,原点 (\(P'\)) が一致するように重ね,
さらに,同じ点が重なるように \(\phi_P\) を変形
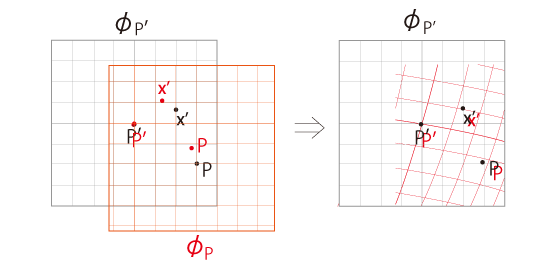
ここで新座標が曲線座標になるのは,射影のしくみによって,二点間の観測される距離が違ってくるからである。
──例えば,\(P,\,P'\) 間の距離の場合だと:
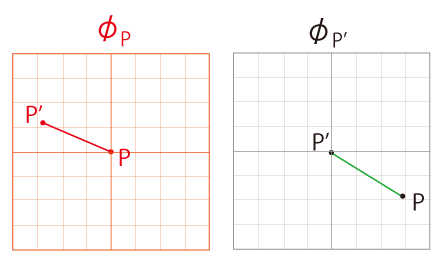
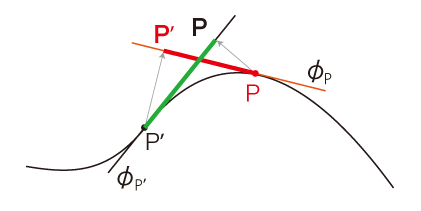
| (1) |
\( \phi_P\) のデカルト座標の基底を,
\[
{\bf E} = \{ {\bf E}_1,\, \cdots,\, {\bf E}_n \}
\]
とする。
この基底に対する座標系を,\(X^i\) 座標系と称する。
|
| (2) |
曲線座標 (上図の赤色のメッシュ) を,\(x^i\) 座標系と呼ぶ。
|
| (3) |
曲線座標の基底──局所直線基底──を,
\[
{\bf e} = \{ {\bf e}_1,\, \cdots,\, {\bf e}_n \}
\]
で表し,基底 \({\bf E}\) に対する各 \( {\bf e}_i \) の座標を
\[
( e_i^1,\, \cdots,\, e_i^n )
\]
とする──即ち,
\[
{\bf e}_i = e_i^{\ 1}\, {\bf E}_1 + \cdots + e_i^{\ n}\, {\bf E}_n \quad ( i = 1, \cdots, n )
\]
|
|















