リーマン多様体の地図 \(\phi_P\) は,つぎの二つを合わせて使う:
- \( P \) から観える世界を写した地図
- 別の地図の読み込み
a は,直線座標──正規直交座標 (デカルト座標) ──に順う。
b は,結果的に,曲線座標になる。
地図 \(\phi_P\) を地図 \(\phi_P'\) から読み込む:
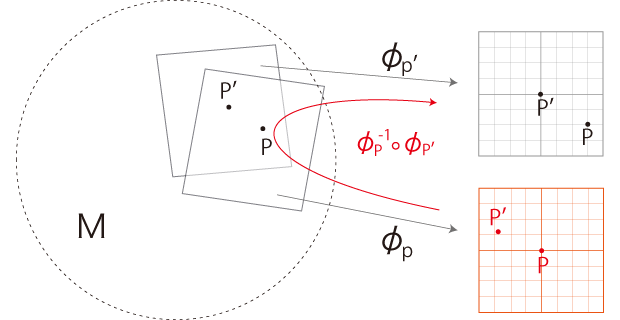
読み込まれた \(\phi_P\) のデカルト座標が曲線座標になる:
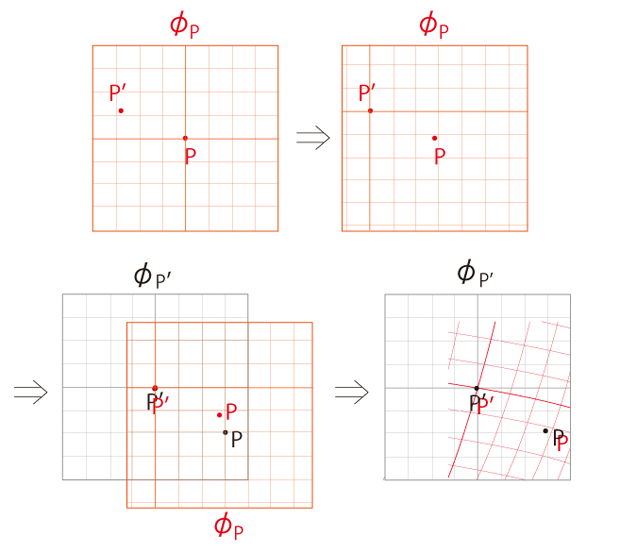
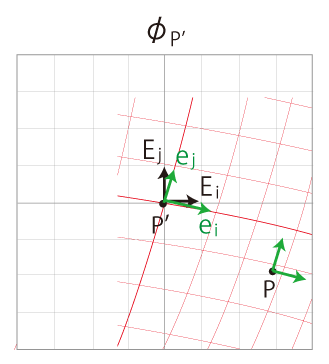
| (1) |
デカルト座標の基底を,
\[
{\bf E} = \{ {\bf E}_1,\, \cdots,\, {\bf E}_n \}
\]
とする。
この基底に対する座標系を,\(X^i\) 座標系と称する。
|
| (2) |
曲線座標 (上図の赤色のメッシュ) を,\(x^i\) 座標系と呼ぶ。
|
| (3) |
曲線座標の基底──局所直線基底──を,
\[
{\bf e} = \{ {\bf e}_1,\, \cdots,\, {\bf e}_n \}
\]
で表し,基底 \({\bf E}\) に対する各 \( {\bf e}_i \) の座標を
\[
( e_i^1,\, \cdots,\, e_i^n )
\]
とする──即ち,
\[
{\bf e}_i = e_i^{\ 1}\, {\bf E}_1 + \cdots + e_i^{\ n}\, {\bf E}_n \quad ( i = 1, \cdots, n )
\]
|
リーマン多様体で主題になる「座標変換」は,以上の基底の間の座標変換であり,これに限る。
「リーマン多様体/幾何学」のテクストには,きまって極座標,球面座標,円筒座標の類が出てくるが,これはつぎの二つが混在している状態である:
学習者は,これにも躓く。
「この幾何学的対象がリーマン多様体のモデルになるのは,どんな趣旨によってか」の説明が無くて導入されるからである。
テクストの書き手も,極座標等を勘違いして取り上げているふしがある。
局所直交座標と極座標の変換のようなのを「リーマン多様体の座標変換」にしているからである。
|


