さて,この記述は,どんな構造になっているのか。 以下のように考える。 多様体 \(M\) に対し,集合 \(E\) と関数 \( f : M \to E\) が立っている。 各地図 \(\phi\) に対し,つぎの図式を可換にする関数 \( F_{\phi} \) が存在する── 実際,\( F_{\phi} = f \circ \phi^{-1}\) がこれである: 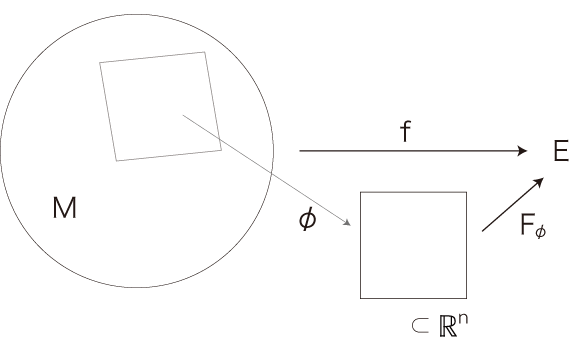
各 \( {\bf p} \in \phi \) には,\( F_{\phi}\) によって \(E\) の要素が対応している。 これは,\( \bf p\) の「\(f\) 情報」ということになる。 ここで,「場」のことばを,つぎのように導入する:
多様体 \(M\) の地図帳は, \(M\) の解析のために導入されているものである。 \(M\) の解析は,\(M\) に関する情報の解析である。 そして「\(M\) に関する情報」を,ここで述べた構造のものとして考えようというわけである。 |