リーマン多様体 \( M\) は,「曲がった空間」の主題化である。
そしてその「曲がった空間」は,つぎの形で表現されるものである。
《点 \(P\) の地図 \(\phi_P\) を点 \(P'\) の地図 \(\phi_{P'}\) に読み込むと,
\(\phi_P\) のデカルト座標が曲線座標になって現れる》
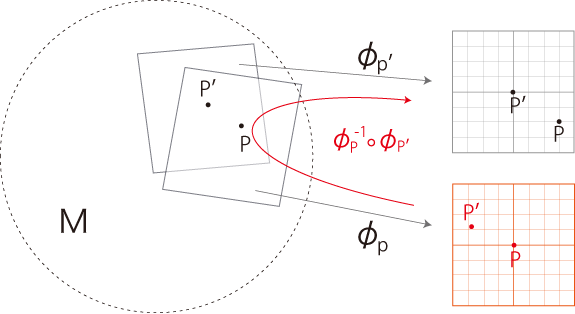
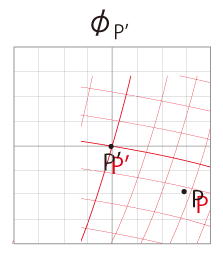
空間が曲がっているので,距離は曲線の長さになる。
これの測度は,<距離の微分を継ぎ足す>を<地図を接ぐ>を以て行うものになる。
──測度は,<微分>で考えるものである。
2点\(P,\,P'\) 間の距離──微小な距離──を測る。
これは,つぎのように考える:
地図 \(\phi_P\) を地図 \(\phi_{P'}\) に読み込む。
\(\phi_{P'}\) に現れた \(P,\,P'\) 間の距離を,デカルト座標で読む。
\(P,\,P'\) 間の距離は,なぜ \(\phi_P\) ではなく \(\phi_{P'}\) 上で読まれるのか。
物事の進行は,このようになるからである。
\(P'\) は \(P\) の後に続く存在であり,本来,\(P'\) が現れたところで \(P,\,P'\) 間の距離の対象化となるわけである。
\(P,\,P'\) 間の距離を求める。
\(\phi_P\) を \(\phi_{P'}\) に読み込む:
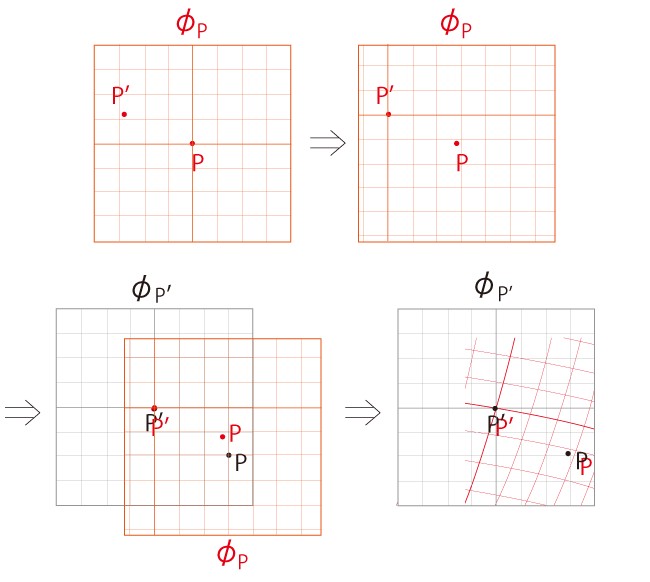
図は,デカルト座標 \(X^i\) と曲線座標 \(x^i\) のメッシュを描いているので,座標をそのまま読めそうに思わせてしまう。
しかし実際は,座標のメッシュは計算して出てくるものである。
そしてその計算は,いまから行おうとする計算と同じものである。
このときわかっているとするものは,\(\phi_{P'}\) 上の \(P\) の \(x^i\) 座標
\[
( a^1,\,\cdots,\, a^n )
\]
である。
というのも,これは \(\phi_P\) における \(P'\) の \(X^i\) 座標の符合を逆にしたものだからである。
これの \(X^i\) 座標
\[
( A^1,\,\cdots,\, A^n )
\]
は,座標変換の式に順い,つぎのようになる:
\[
\left(
\begin{array}{c}
A^1 \\
\vdots \\
A^n \\
\end{array}
\right)
\ =\
\left(
\begin{array}{ccc}
\frac{\partial X^1}{\partial x^1} & \cdots & \frac{\partial X^1}{\partial x^n} \\
& \cdots & \\
\frac{\partial X^n}{\partial x^1} & \cdots & \frac{\partial X^n}{\partial x^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
a^1 \\
\vdots \\
a^n \\
\end{array}
\right)
\]
そこで,\(P,\,P'\) 間の距離 \(s\) は,
\[
\begin{align*}
s^2 &= \sum_{k} (A^k)^2
\\
&= \sum_{k} \left( \sum_i \frac{\partial X^k}{\partial x^i} a^i \right)^2
\\
&= \sum_{k} \left( \sum_{i,j} \frac{\partial X^k}{\partial x^i} \frac{\partial X^k}{\partial x^j} a^i a^j \right)
\\
&= \sum_{i,j} \left( \sum_{k} \frac{\partial X^k}{\partial x^i} \frac{\partial X^k}{\partial x^j} \right) a^i a^j
\end{align*}
\]
ここで,
\[
g_{ij} = \sum_{k} \frac{\partial X^k}{\partial x^i} \frac{\partial X^k}{\partial x^j}
\]
とおいて,つぎの式を得る:
\[
s^2 = \sum_{i,j} g_{ij} a^i a^j
\]
はじめに述べたように,距離の計算は「微分」で考えることになる。
よって,最終的に提示する式は,つぎのものである:
\[
ds^2 = \sum_{i,j} g_{ij} dx^i dx^j \\
\quad g_{ij} = \sum_{k} \frac{\partial X^k}{\partial x^i} \frac{\partial X^k}{\partial x^j}
\]
ここまで「距離を求める」と言ってきたが,いまよりは「計量」の言い回しを用いる。
──実際,「距離「も「計量」も,英語では同じ metric である。
|


