Up 「真っ直ぐ進む」 作成: 2018-01-12
更新: 2018-03-05

    リーマン多様体 \( M \) の上を，点 \(P\) を出発点にして真っ直ぐ進むことを考える。

    地図 \( \phi_P\) を開き，この上にベクトル \(\bf A\) を措く：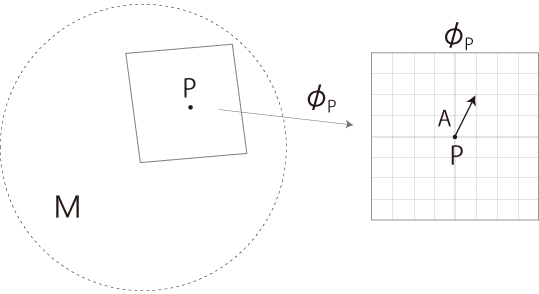

    そして，
      1. \( \phi_P\) の上で，\(\bf A\) をこれの方向に \(d{\bf x}\) だけ進める。
      2. 進めた先の点 \(P'\) の地図 \( \phi_{P'}\) を開き，
      地図 \( \phi_P\) を読み込む。
      3. \( \phi_{P'}\) の上で，\(\bf a\) (\(\bf A\) の像) をこれの方向に \(d{\bf x}\) だけ進める。
      4. この手順を繰り返す。

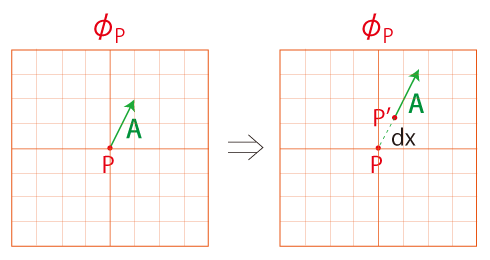
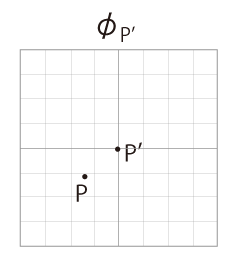
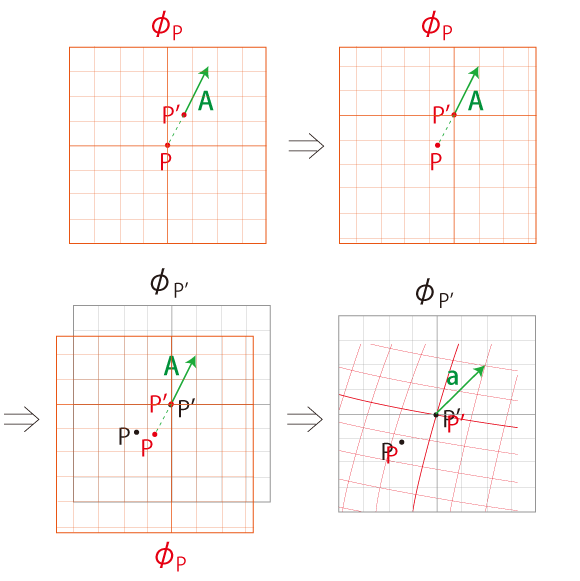
      そうすると，開いた地図 \( \phi_P\) 全体に対する \( P\) 全体は, 「\(d{\bf x} \to \bf 0\)」と合わせるとき，\( M \) の上を真っ直ぐに進んだ軌跡になっているはずである。
      ──実際，「真っ直ぐ」は，これ以外の意味では考えられない。


      この「真っ直ぐに進む」によってできる線を，「測地線」と呼ぶ。
      上の場合は，ベクトル \( A\) から始めたので，「A に順う測地線」ということになる。

      地図を接ぐこの手順は，「実行できる操作」である。
      これは，「測地線」は存在定理を俟つまでもなく存在する，ということである。