fを,二つの量の系 ( (量1, +), ×, (数, +, ×) ),( (量2, +), ×, (数, +, ×) ) の間の比例関係とする。
量1,量2 からそれぞれ要素を「単位」として固定し,fから「値の対応」を導く。
するとこれは,一定数倍の関数になる。
即ち,「y=ax」と表現されるものになる。
いま,上の二つの量の系が,つぎのように位の系に含まれているとする:
( 位1, +, ( (量1, +), ×, (N, +, ×) ) )
( 位2, +, ( (量2, +), ×, (N, +, ×) ) )
|
そして,Fを,比例関係f: 量1 → 量2 を伴うアフィン関係: 位1 → 位2 とする。
──Fとfは,つぎの関係にあった:
F( P′ ) − F( P ) = f( P′ − P ) ( P, P′ ∈ 位1 )
|
ここで,比例関係fから数の対応「y=ax」を導いたのに倣って,アフィン関係Fから数の対応を導くことを考える。
これは,どのような形のものになるか?
結論から言うと,「yーq=a (xーp)」 の形になる。
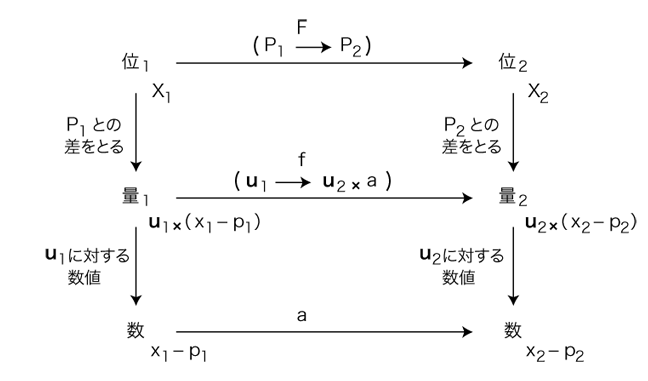
Fから数の対応を導く考え方は,量1,量2 からそれぞれ一つの要素を「単位」として固定することと併せて,位1,位2 からそれぞれ一つの要素を「基準」として固定するというものである。
即ち,以下のようになる。
位1,位2 の枠をそれぞれ (O1, u1), (O2, u2) とする。
いま,
f(u1)
= u2 × a
F(P1) = P2
P1 = O1 + p1,
p1 = u1 × p1
P2
= O2 + p2,
p2
= u2 × p2
とし,
F(X1) = X2
X1 = O1 + x1,
x1 = u1 × x1
X2
= O2 + x2,
x2 = u2 × x2
とするとき,
f(X1 ー P1 )
= F( X1 ) ー F( P1 )
= X2 ー P2
ここで,
X1 ー P1
= (O1 + x1) ー
(O1 + p1)
= x1 ー p1
= u1 × x1 ー
u1 × p1
= u1 ×
(x1 ー p1)
同様に,
即ち,fで,
u1 ×
(x1 ー p1)
に
u2 ×
(x2 ー p2)
が対応する。
そしてこのことは,つぎを意味する:
こうして,Fから導かれる数値の対応は,「 (x1 ー p1) × a
= x2 ー p2」である。
| 例. |
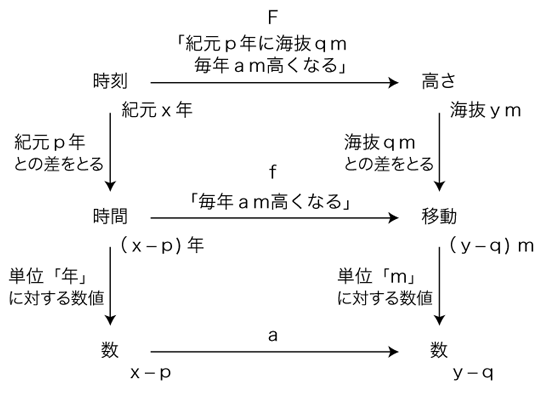
時刻:( 時刻, +, ( (時間, +), ×, ( , +, ×) ) ) と高さ:( 高さ, +, ( (移動, +), ×, ( , +, ×) ) ) と高さ:( 高さ, +, ( (移動, +), ×, ( , +, ×) ) ) を考える。 , +, ×) ) ) を考える。
時刻の枠に (紀元, 年) をとり,高さの枠に (水準, m) をとる。
比例関係f:時間 → 移動 とアフィン関係F:時刻 → 高さ を,つぎのように定める:
f(年) = m × a(「毎年am高くなる」)
F(紀元p年) = 海抜qm
F(紀元x年) = 海抜ym
このとき,
f( 紀元x年 ー 紀元p年 )
= 海抜ym ー 海抜qm
ここで,
紀元x年 ー 紀元p年
= 年 × (x ー p)
海抜ym ー 海抜qm
= m × (y ー q)
即ち,fで,
年 × (x ー p)
に
m × (y ー q)
が対応する。
そしてこのことは,つぎを意味する:
こうして,Fから導かれる数値の対応は,「 (x ー p) × a = yーq」である。
|
以上見てきたように,「量の比例関係の上の位対応」 に対し「基準・単位」を固定することで導かれる関数:数 → 数 は,直接的には「(x ー p) × a = yーq」であり「y=ax+b」ではない。
── b=qーp×a とおき直すことで「y=ax+b」になる。
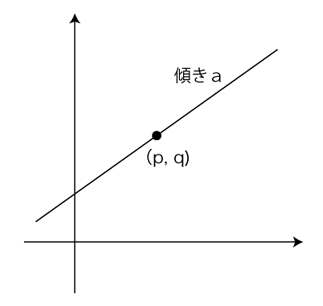
また,「1次関数」のグラフの解釈が,つぎのように違ってくる。
「(x ー p) × a = yーq」
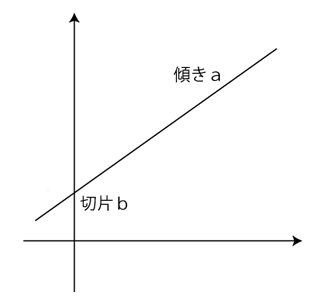
「y=ax+b」
|



 , +, ×) ) ) と高さ:( 高さ, +, ( (移動, +), ×, (
, +, ×) ) ) と高さ:( 高さ, +, ( (移動, +), ×, (