そしてこれが,《1次関数でないものを「1次関数」として授業する》になってしまう。 数学の主題は,これの出自に「卑近」があり,この「卑近」を教えることが主題の意味を教えることになる。 よって,「1次関数」の素材を「卑近」に求めるという姿勢それ自体は,まったく正しい。 問題は,「卑近」は「日常生活の中」とイコールではないということである。 教員が「1次関数」の素材を日常生活の中に求めようとするときは,きまって「段々に増加・減少」を「1次関数」にしてしまう。 「段々に増加・減少」は,日常生活の中にいろいろある。 例えば「料金設定」はそうである。そしてこの類が「1次関数」の素材にされる。 日常生活の中の「段々に増加・減少」は,「同じ段々で増加・減少」が基本になっている。 「同じ段々」になるのは,階段の一段一段が同じにされるのと同様の理屈である。 段を同じにしないことは,不具合・混乱のもとになる。 この「同じ段々で増加・減少」を表現する関数は,「1次関数」か? そうではない。 「段々」をグラフにする関数も,「階段関数」の名で数学の内容となるものであり,そしてそれは「1次関数」とはいっしょにされない。 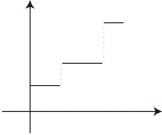
しかし,等速運動を1次関数に乗せるロジックは,存外難しい。 実際,等速運動が<経過時間-速度>の軸だと定値関数,<経過時間-移動距離>の軸だと1次関数になる理屈は,教員養成系大学数学教育専攻の学生でも,述べるのに難儀する (ざっくり言ってしまえば,述べられない)。 「1次関数」は,「卑近」のところですでに,中学数学には荷の重い内容になってしまうわけである。 |