1.「2個の3個は何個?」 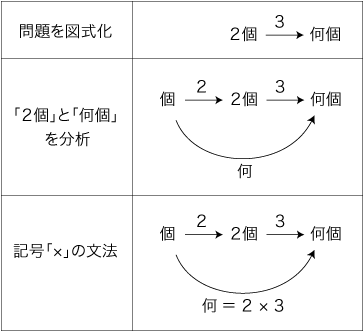
2.「2mの3倍は何m?」 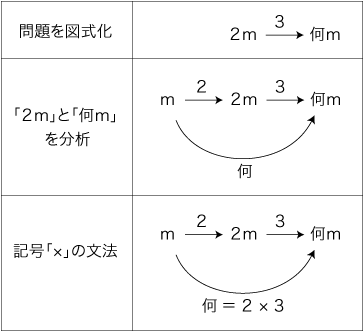
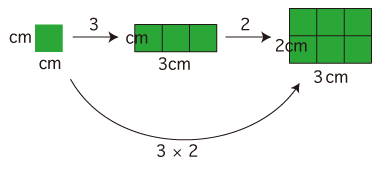
このように,つぎが「文章題から数の積の式を立てる」のプロセスになる: 3.「タテ2cm,ヨコ3cm の長方形の面積は何 cm2?」 この問題は,「単位の倍の倍」のつくり方が2つある: 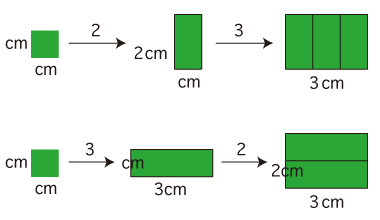
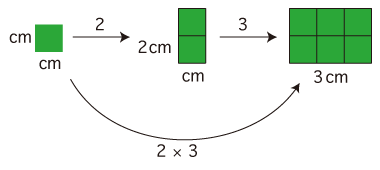
「かけ算の順序」論議/論争は,延々と終わらない。 それは,「文章題から数の積の式を導く」のプロセスを,数学で考えられないためである。 このプロセスを,もう一度記しておく: 「かけ算の順序」論議/論争は,《文章題から「単位の倍の倍」を導く》の考えをもたない。 そのかわりに,非数学のモンスター論理が様々に展開される。 実際,「単位の倍の倍」が一旦立てられれば,数学を知っている者なら,これを数の積の式に還元する推論は一意になる。 特に,かけ算の順序は一意に決まる。 以上のように,「かけ算には順序がある」「かけ算には順序がない」では,「かけ算には順序がある」が正しい。 |