一方の2倍,3倍,‥‥に他方の2倍,3倍,‥‥が対応する」 この定義は,一見,有理数倍および実数倍を欠く不完全な定義に見える。 しかし実際には,有理数および実数○に対する「一方の○倍に他方の○倍が対応」がこの定義から導かれるので,定義として問題ない ( 証明は数の拡張に乗せていくものである → 証明)。 いま,f:量1 → 量2 を比例関係とする。 「一方の○倍に他方の○倍が対応」は,式で書くとつぎのようになる:
つぎのステージは,量1,量2 それぞれにおいて,単位 u1,u2 を固定することから開始される。 量1 の任意の要素q1 は,u1 の何倍の形に書ける:
量2 の場合も同様である。 そこで,f:量1 → 量2 からは,数値の対応が導ける。 この対応をφ(ファイ) とする:
さて,fには「一方の○倍に他方の○倍が対応」のきまりがある。 そこで,「fから導かれるφにも何かきまりが見出されるはずだ」と考えるのは,自然である。 そして,きまりを求めてみると,「一定数倍」が求まる:
これが,学校数学の「y=ax」であり,aを「比例定数」と呼ぶ。 「y=ax」の要点は,つぎの2つである: そして,以上の内容は「線型空間」の数学と対比できるものになる: 実際,この対比は,実数係数の「量」と「1次元線型空間」が同じものになることに因っている。 (そして実数係数では,「比例定数a」は「1×1行列 (a)」と同じ!) 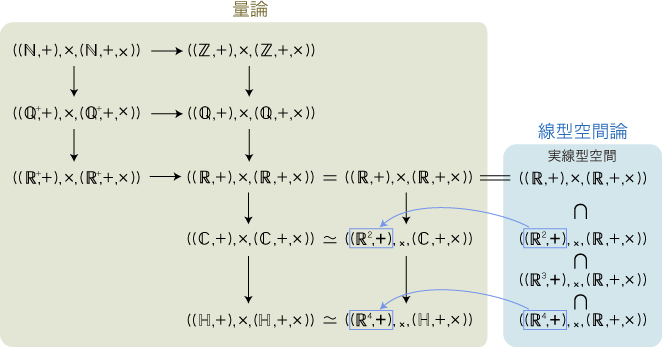
「一方の2倍,3倍,‥‥に他方の2倍,3倍,‥‥が対応する」から,整数,有理数,実数係数での「一方の○倍に他方の○倍が対応」が導かれることの証明:  『「数とは何か?」への答え』): 『「数とは何か?」への答え』):
即ち,Q は0でないu∈Qに対する{ u×n|n∈N}の形になり,つぎの対応が ( ( N, + ), ×, ( N, +, × ) ) と ( ( Q, + ), ×, ( N, +, × ) ) の間の同型になる:
Nが負数をもつ数 ( e.g.  , , , ,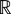 ) の場合,各q∈ Q には対称元 ーqがある。さらに,つぎが成り立つ: ) の場合,各q∈ Q には対称元 ーqがある。さらに,つぎが成り立つ:
q=u × aとする。 q × n=u × (a×n)。 a×nと ー(a×n) は,互いに対称元。 そこで,u × (a×n) とu × (ー(a×n)) は,対称元。 また,u × (ー(a×n)) と (−u) × (ー(a×n)) は,足して0になるので,対称元。 そして,
量の系 ( ( Q1, + ), ×, ( N, +, × ) ), ( ( Q2, + ), ×, ( N, +, × ) ) と関数 f:Q1 → Q2 において,つぎが成り立っているとする:
つぎが成り立つ:
以上の準備のもと,これより本題の証明に入る。 (1) Nが整数の場合 f(q × (ー2)) =f(q) × (ー2) を示す:
= f((ーq) × 2) = f(ーq) × 2 = (ーf(q)) × 2 = f(q) × (ー2) (2) Nが分数 (正の有理数) の場合 f(q × 2/3) =f(q) × 2/3 を示す:
これは,つぎの条件を満たすc∈Q1 が存在するということ:
c × 2 =q′
f(c) × 2 =f(c × 2) =f(q′) (3) Nが実数の場合 f(q × π) =f(q) × π を示す:
先ず,{q ×nk|k=1,2,‥‥}が,Q1 における Cauchy列になり,これより{f(q ×nk)|k=1,2,‥‥}が,Q2 における Cauchy列になる。 そして,これが定めるQ2 の要素はf(q ×π)。 また,Cauchy列{f(q ×nk)|k=1,2,‥‥}は,「Nが有理数の場合」に還って,{f(q) ×nk|k=1,2,‥‥}であり,そして,{f(q) ×nk|k=1,2,‥‥}が定めるQ2 の要素はf(q) ×π。 よって,f(q × π) =f(q) × π。 |