個数の場合,生活体験的ないし生理的に,<個>がほぼ一意的に定まる。そのため,個数とそれを扱う自然数が即応するような感じになる。そこで,「数指導はタイルで」のような考えも出てくることになる。 「数指導はタイルで」では,例えば「2」のイメージ (理解シェマ) はつぎのようになる: 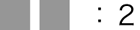
「数指導はタイルで」は,数・量が自然数・個数で考えられていることによる。 そして,自然数・個数のところでしか持ち堪えられない。 実際,分数になると,個数と自然数の即応のような<量と数の即応>という関係は,もはや立たなくなる。 「数は量の比」につかねばならなくなる。 しかし,「数は量の抽象」は,「数は量の比」を退けることで自分を立てているわけであるから,「数指導はタイルで」を自然数より先の数にもなんとか延長しようとする。 そしていろいろ無理を重ねていく。 |