「数は量の抽象」で「割り算には等分除と包含除がある」が言い出されるのは，自然数・個数で以て数・量を考えているからである。 実際，「割り算には等分除と包含除がある」は，自然数・個数のところでしか持ち堪えられない。 自然数・個数で考えているにしても，どうして「割り算には等分除と包含除がある」となるのか？ 「数は量の抽象」では，自然数の割り算も「量計算の抽象」として意味づけなければならない。 そしてこれより，自然数の割り算に「等分除・包含除」の区別がつけられることになる。 数学では，「割り算」とは記号「÷」の文法のことであり，そしてつぎが「÷」の文法である：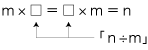 
さて，二つの式 ｍ×□＝ｎ，□×ｍ＝ｎ は，つぎの形式の中に現れる： 
自然数の場合，左の形式は「包含」の問題に適用できる：
「12人に対し，3人がけの椅子をいくつ用意すると全員すわれる？」 そして，右の形式は「等分」の問題に適用できる：
「12人が3つの長椅子に同じ人数だけ座ると，一つの長椅子には何人？」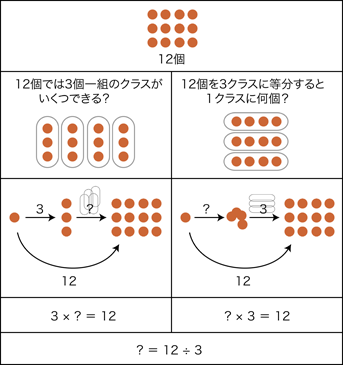 
「ｎ÷ｍ」に「等分」と「包含」の二つの意味があるのではない。 ──つぎのようになる：
要点は，計算の道具と計算の対象の区別である。 ところが，「数は量の抽象」論は，「計算の道具は計算の対象の抽象」論である。 そこで，「数は量の抽象」論では，「ｎ÷ｍ」に直接「等分」「包含」の２つの意味を考えてしまうことになる。 学校数学での自然数の割り算の指導は，この「等分除と包含除」である。 「12 ÷３」の意味は？と問われた生徒は，これが適用される等分ないし包含の問題を答えて，正解したことになる。 「3/2 ÷ 4/5」の意味は？と問われると，もう答えられない。──正負の数や複素数の場合は，言わずもがな。 そして，これは教員においても同じである。  鳥瞰図 (「積・商の立式」のロジック)
|