これに対比して,「数は量の抽象」の立場に立つ「割合の問題の解法」を,以下に示す: |
| 問題 | 2gの何倍が6gか? | 2gの3倍は何gか? | 何gの3倍が6gか? |
| 「割合」的表現 | 2gに対する6g の割合は? |
2gに対する何g の割合が3か? |
何gに対する6g の割合が3か? |
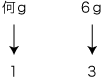
| もとにする量を 「1と見る」 |
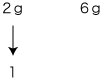 |
 |
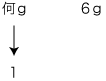 |
| 比較する量の抽象に なる数が, 割合になる (「割合」の定義) |
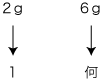 |
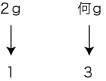 |
 |
| 「比の3用法」(公理) の適用 |
第1用法より: 何=6g÷2g |
第2用法より: 何g=2g×3 |
第3用法より: 何g=6g÷3 |
| 数の「×・÷」は 量の「×・÷」の抽象 |
何=6÷2 | 何=2×3 | 何=6÷3 |
「数は量の抽象」の立場では,数は量である。 「割合」も,量として定義されねばならない。 そこで,上のような「割合」の定義になる。 ──特に,「倍」としてつぎのように描かれるものには,ならない:  「比の3用法」は,事物の存在法則のような位置づけの<公理>である。 実際,「数は量の抽象」の立場は,量を実体概念にする。 「比の3用法」を記述している「×・÷」も実体概念である。 これを数学的に定式化しようとしたら,没論理ないし循環論法になる。 「何=6g÷2g,何g=2g×3,何g=6g÷3」から「何=6÷2,何=2×3,何=6÷3」を導くところも,数学的には没論理である。 特に,記号の混乱が,先ず退けられるものになる。 すなわち,数学では,量に対する数を,量の作用域として定義する。 「×」は,数の「内算法 (演算)」である。 量の内算法として定義されるのは,加法のみである。 しかし,「数は量の抽象」の立場では,量には「積」がある。 「何=6÷2,何=2×3,何=6÷3」も,量の演算として意識されている。 |