自然数を使う量では,「個」と呼ばれる「部分を考えない量」を想定したが,「任意に部分を考えられる量」を扱いたくなったときに,分数がつくられる。 さらに,正逆2方向 (1次元自由) の量 (イメージとしては直線上のベクトル) を扱いたくなって,正負の数がつくられる。 2次元自由の量 (イメージとしては平面上のベクトル) を扱いたくなって,複素数がつくられる。 3次元自由の量を扱いたくなって,四元数がつくられる。 ──といった具合である。 以下,「数と量」のカテゴリーがどのようであるかを押さえておく。 ここでは,「数・量のカテゴリーは一通りでない」ということを見られたい。 「数と量」のカテゴリーをここで押さえておくことの趣旨は,自分が「数と量」としているものが,全体のどの辺りにあるのかを知るということである。 実際,ひとはたった一つの「数と量」を論じて,「数と量」の世界を論じているつもりになるものであるから。 数学では,量をつぎのカテゴリー区分でそれぞれ対象化していることになる: 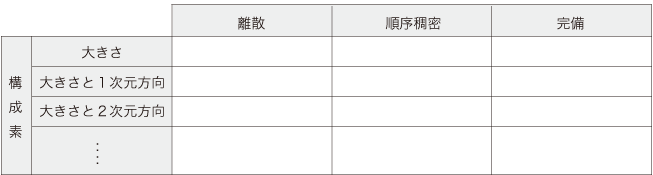
ただし,このうち「意味のあるカテゴリー」として実際に対象化しているのは,つぎのものである:  このカテゴリーを実現するものは,数(系) である。 複数のカテゴリーがあるので,複数の数(系) が必要になる。 これをつぎのようにつくっていく──矢線の意味は「導出・拡張」である:  数学の「量」は,形式である。 この形式を,数(系) を素材にしてつくる: (  数が量をつくる (『「数とは何か?」への答え』)): 数が量をつくる (『「数とは何か?」への答え』)):
 そして以降,「数」を「量の比」として使っていくことになる。 上の表から特に「比」の部分を取り出したのが,つぎの表である── これは,<量のカテゴリー>と<比として使われる数(系)>の対応を示す表になる:  |