Up 「数直線」の授業設計  

「数直線」の授業設計は，どういうことを考え，そしてどのように進めるか？
以下は一つの例です。

  1. 主題をとらえる

      「正負の数」の単元における「数直線」の授業設計は，「数直線」の意味をとらえることから始まります。

      一般に，主題の意味を正しくとらえることは，ひじょうに困難です。
      深く考えると同時に，変てこな考え方に陥っていないかを警戒することが必要です。 （よく知らないことを深く考えると，たいてい変てこな考え方に陥ります。）

      「数直線」の意味は，つぎのようになります：

        すべての数を直線上に配置する──数が異なれば位置も異なるように。
        (「配置」の意味は，数に直線上の点を対応させるということ。)

      　註 : さらに加えるならば：
      　 数の大小の順序関係に，配置の順序が対応するようにする。 ──すなわち，数が大きくなるとその位置が一方の方向にずれていく，という具合にする。
      （一般的に言うと，「数の自然な位相と埋め込み先の空間の位相に関して，同相対応であるようにする」)
      しかしこれは，「満たしたい条件」と見ることもできますが，「配置が規則的でなければならないことから出てくる自然な結果」と見ることができます。 したがって，「数直線」の意味には含めなくていいでしょう。


  2. 授業の型を決める

      「すべての数を直線上に配置することができるか？」 ──答えを知ってしまえば簡単ですが，知らない者にとっては，これはたいへんな難問です。
      そして，これの解決を自ら実践することで，上に示した「数直線」の本質もわかってきます。

      そこでこの授業は，「課題解決」の形に組み上げれば，素直な設計になります。


  3. 「課題提示」の内容を決める

      「課題解決」の形に授業を組み立てることにしたら，つぎに「生徒に与える課題は，どのようなのがいいか？」と考えることになります。
      自問することは，「主題の本質が示される課題は？」です。

      「数直線」の場合は，「数直線」の意味を問うことばがそのまま「主題の本質が示される課題」になります。 すなわち，つぎの発問がそのまま「主題の本質が示される課題」の提示になります：
        「すべての数を直線上に並べられないか？」
      あるいは，
        「実は，すべての数を直線上に並べることができる。
        　いまから自分でその方法を考え出してみよう。        」


  4. 「問題解決の指導」の内容を決める

    • 最初に，生徒に試行錯誤させます。

      • これをさせて，どんな問題であるのかをつかませる。
        ──問題の勘所・要所をつかませる。
      • 「きまりが必要」の意識をもつことが，ここのゴール。

    • これ以降，指導は「数直線を書く」の構造化 (構造の取り出し) を行いながら，問題解決のゴールへと進みます。

        この構造化の要素となるものは：

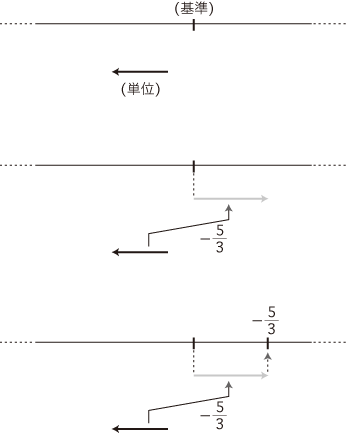
        1. 「基準」と「単位」の導入
        2. 数に直線上の点を対応させる規則
            「数ｎと対応するのは，基準から単位のｎ倍の位置の点」




    • この指導では，参考にするものとして，高さや時刻の表現 (位表現) を使えます。

    • この指導では，
        「基準・単位の恣意性」
        「基準・単位の取り方によって，数直線の形が変わる」
      も主題の一部になります。
      これは「生徒各々に作業させ，結果を互いに紹介させる」の方法を用いることで，自ずと主題にのぼらせることができます。

    • 整数から始めるのも，分数から始めるのも，両方あります。
      ただし，整数から始めるのは，生徒にとって課題への入りがやさしくなりますが，「数＝比」のとらえに生徒を導くのが難しくなります。
      逆に，分数から始めれば「数＝比」をまともに扱うことになります。

      素人考えでは「やさしいから難しいへ」がよいとなります。
      しかし，「やさしいから難しいへ」は，
        「＜本質をそらす形でやさしくしたもの＞から入って，
        　あとで本質に入る」
      ということです。 そして「本質をそらす形でやさしく」は，変な癖を頑固につけてしまうことになるので，「あとで本質に入る」はひじょうに困難になります。

      「本質をそらす形でやさしく」をやった後の段はもう無いというのなら，これでもいいでしょう。しかし「本質に入る」が必須としてあり，そして本質をそらさない形がこれができるのなら，本質をそらさない形をやるべきです。
      この理由から，ここでは「数直線」の課題解決に対し，「整数と分数を合わせて」の方法をとるします。（実際，直接分数から入ることは可能です。)


  5. 「数学的表現を与える」の内容を決める

    • 行ったこと・獲得したことの内容を的確に言い表すことば (数学的表現) を，これまた学習内容として，生徒に与えます。

        「的確な表現」としての数学的表現は，歴史の中で構造化され磨かれてきたことばであり，学習内容として与えられるものになります。
        特に，これは「要約」とは違います。


  6. 「まとめ」の内容を決める

    • 課題解決行動を終えたばかりの生徒にとって，行ったこと・獲得したことは，まだ整理されていません (バラバラな状態)。
      これの整理が，この「まとめ」のステージで行うことです。