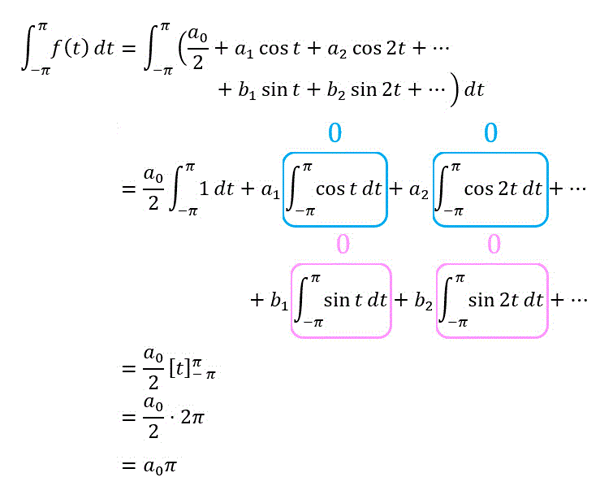https://www.momoyama-usagi.com/entry/math-cp-analysis07
から引用
工学部の数学で、「フーリエ級数展開」という言葉を聞いたことがある人は多いかと思います。
しかし、「あれなにやってんだ!?」と思った人もいるかもしれません。
今回はそんな「フーリエ級数展開」について仕組み・計算方法についてわかりやすく説明していきたいと思います。
1.フーリエ級数展開とは
まずは下のグラフをみてみましょう。
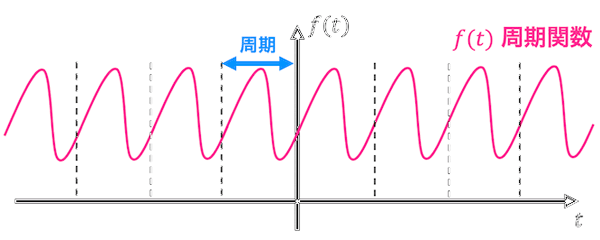
この関数のグラフはある一定の間隔で同じ形の曲線を繰り返していますね。
このような関数のことを周期関数と呼びます。
数式で書くと、すべての自然数 \( k \) に対し、\[
f(t) = f(t+kT)
\]となるような関数のことを周期 \( T \) の周期関数と呼びます。
フーリエ級数展開は、周期関数を皆さんおなじみの偶関数 \( \cos \) と奇関数 \( \sin \) の2つに分解して表そう! というやつです。
2.フーリエ級数展開で用いる三角関数の積分
フーリエ級数展開の公式を説明する前にまずは下の公式を導出するために必要な三角関数の積分の復習をしましょう。
三角関数の加法定理・倍角の公式・積和の公式などを用いた積分を行います。
※今回は \( - \pi \) から \( \pi \) までの積分範囲としていますが、\( 0 \) から \( 2 \pi \) としても同じ結果が得られます。
まずは \( \cos nx \), \( \sin nx \) 単体の積分を見てみましょう。
フーリエ級数展開で用いる三角関数の公式1
\[
\int^{\pi}_{- \pi} \cos nx \ dx = 0 \]\[ \int^{\pi}_{- \pi} \sin nx \ dx = 0
\]が成り立つ。
[導出]
\[\begin{align*}
\int^{\pi}_{- \pi} \cos nx \ dx & = 2 \int^{\pi}_{0} \cos nx \ dx
\\ & = 2 \left[ \frac{1}{n} \sin nx \right]^{\pi}_{0}
\\ & = 0
\end{align*}\]と計算できる。
また、\( \sin nx \) は奇関数なので\[
\int^{\pi}_{- \pi} \sin nx \ dx = 0
\]となる。
つぎに、\( \cos \) と \( \sin \) が2つ組み合わさったバージョンを見ていきましょう。
フーリエ級数展開で用いる三角関数の公式2
\[
\int^{\pi}_{- \pi} \sin mx \cos nx \ dx = 0
\]となる。
また、\( m \not = n \) のとき、\[
\int^{\pi}_{- \pi} \sin mx \sin nx \ dx = 0 \]\[
\int^{\pi}_{- \pi} \cos mx \cos nx \ dx = 0
\]となる。
[導出]
\( \sin mx \) は偶関数、\( \cos nx \) は奇関数なのでその積は奇関数となる。
よって、\[
\int^{\pi}_{- \pi} \sin mx \cos nx \ dx = 0
\]となる。
また、\[\begin{align*}
\sin mx \sin nx = \frac{1}{2} \cos(m-n) x - \frac{1}{2} \cos(m+n) x
\end{align*}\]なので、\[\begin{align*} &
\int^{\pi}_{- \pi} \sin mx \sin nx \ dx
\\ = & \ \frac{1}{2} \int^{\pi}_{- \pi} \cos(m-n) x \ dx - \frac{1}{2} \int^{\pi}_{- \pi} \cos(m+n) x \ dx
\\ = & \ 0
\end{align*}\]と計算できる*1。
同じようにして、\[\begin{align*}
\cos mx \cos nx = \frac{1}{2} \cos (m-n) x + \frac{1}{2} \cos (m+n) x
\end{align*}\]なので、\[\begin{align*} &
\int^{\pi}_{- \pi} \cos mx \cos nx \ dx
\\ = & \ \frac{1}{2} \int^{\pi}_{- \pi} \cos(m-n) x \ dx + \frac{1}{2} \int^{\pi}_{- \pi} \cos (m+n) x \ dx
\\ = & \ 0
\end{align*}\]と計算できる。
最後に公式2の \( m = n \) の場合も確かめておきましょう。
この積分は0にならないので要注意です。
フーリエ級数展開で用いる三角関数の公式3
\[
\int^{\pi}_{- \pi} \sin nx \sin nx \ dx = \int^{\pi}_{- \pi} \sin^2 nx \ dx = \pi \]\[
\int^{\pi}_{- \pi} \cos nx \cos nx \ dx = \int^{\pi}_{- \pi} \cos^2 nx \ dx = \pi
\]となる。
[導出]
\[\begin{align*}
\int^{\pi}_{- \pi} \sin^2 nx \ dx & = \frac{1}{2} \int^{\pi}_{- \pi} ( 1 - \cos 2mx ) \ dx
\\ & = \frac{1}{2} \int^{\pi}_{- \pi} 1 \ dx - \frac{1}{2} \int^{\pi}_{- \pi} \cos 2mx \ dx
\\ & = \frac{1}{2} \int^{\pi}_{- \pi} 1 \ dx - 0
\\ & = \frac{1}{2} \left[ x \right]^{\pi}_{- \pi}
\\ & = \frac{1}{2} \cdot 2 \pi
\\ & = \pi
\end{align*} \]となる。
(途中で公式1を使用しています。)
同様にして、\[\begin{align*}
\int^{\pi}_{- \pi} \cos^2 nx \ dx & = \frac{1}{2} \int^{\pi}_{- \pi} ( 1 + \cos 2mx ) \ dx
\\ & = \frac{1}{2} \int^{\pi}_{- \pi} 1 \ dx + \frac{1}{2} \int^{\pi}_{- \pi} \cos 2mx \ dx
\\ & = \frac{1}{2} \int^{\pi}_{- \pi} 1 \ dx + 0
\\ & = \frac{1}{2} \left[ x \right]^{\pi}_{- \pi}
\\ & = \frac{1}{2} \cdot 2 \pi
\\ & = \pi
\end{align*} \]となる。
以上で確認は終了です。
では実際にフーリエ級数展開の公式を見てみましょう!
3.周期が2πの場合のフーリエ級数展開の公式
では、早速フーリエ級数展開がどんな式なのかをみていきましょう。
こちらで、周期 \( T \) が \( 2 \pi \) の場合について説明し、次の第4章で \( 2\pi \) 以外に拡張したバージョンの2つにわけて紹介しています。
(1) 計算公式
まずは周期関数 \( f(t) \) の周期 \( T \) が \( 2 \pi \) に固定されたバージョンを説明したいと思います。
最初に公式をみてみましょう。
周期2πのフーリエ級数展開の公式
周期 \( 2 \pi \) の区分的に連続な周期関数*2 \( f(t) \) のとき、\[
f(t) \approx \frac{a_0}{2} + \sum^{\infty}_{k = 1} \left( a_k \cos k t + b_k \sin k t \right)
\]と表せる*3。
ただし、フーリエ係数 \( a_k \), \( b_k \) は\[
a_k = \frac{1}{\pi} \int^{\pi}_{- \pi} f(t) \cos kt \ dt \ \ (k = 0,1,2,3, \cdots) \]\[
b_k = \frac{1}{\pi} \int^{\pi}_{- \pi} f(t) \sin kt \ dt \ \ (k = 1,2,3, \cdots)
\]となる。
※積分範囲は \( - \pi \) から \( \pi \) ではなく、例えば \( 0 \) から \( 2 \pi \) としてもよい。
とにかく \( 2 \pi \) 分が長さに入っていればOK*4。
色をつけて公式を少しわかりやすくしてみました!

つまり、周期関数 \( f(t) \) を偶関数 \( \cos t \), \( \cos 2t \), \( \cos 3t \), …… と奇関数 \( \sin t \), \( \sin 2t \), \( \sin 3t \), …… を用いて表せるよってことなのです!
少し難しい用語を使うと、周期関数 \( f(t) \) を偶関数 \( \cos t \), \( \cos 2t \), \( \cos 3t \), …… と奇関数 \( \sin t \), \( \sin 2t \), \( \sin 3t \), …… の1次結合で表せるってことです!
しかし、フーリエ係数 \( a_k \), \( b_k \) の求め方が複雑だったりなぜか初期値が \( \frac{a_0}{2} \) となってたり \( b_0 \) がなかったりしますね。
なぜこんな値になっているのかを下のほうで説明していきましょう。
(i) 初期値の導出 \( a_0 \)
まずは初期値のフーリエ係数 \( a_0 \) の公式導出方法です。
\[
f(t) = \frac{a_0}{2} + a_1 \cos t + a_2 \cos 2t + \cdots b_1 \sin t + b_2 \sin 2t + \cdots
\]の両辺を \( - \pi \) から \( \pi \) で定積分しましょう。
すると、
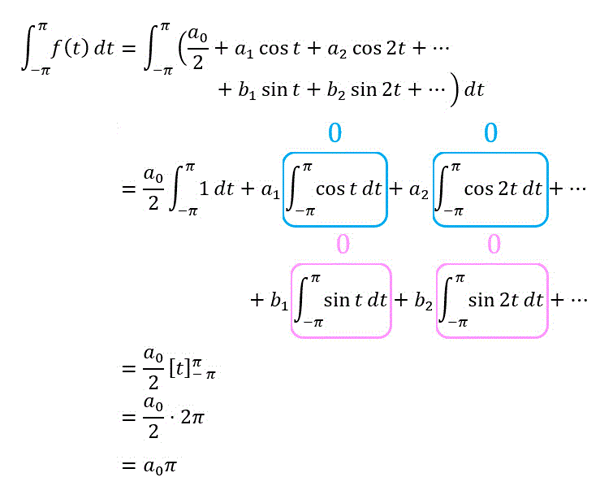
と計算できますね。
よって、\[
\int^{\pi}_{- \pi} f(t) \ dt = a_0 \pi
\]より、\[
a_0 = \frac{1}{\pi} \int^{\pi}_{- \pi} f(t) \ dt
\]と導出できます。
(ii) cos の項の導出 \( a_k \)
つぎに偶関数 \( \cos kx \) のフーリエ係数 \( a_k \) を導出してみましょう。
\[
f(t) = \frac{a_0}{2} + a_1 \cos t + a_2 \cos 2t + \cdots b_1 \sin t + b_2 \sin 2t + \cdots
\]の両辺に \( \cos kt \) を掛けましょう。
すると、\[
f(t) \cos kt = \left( \frac{a_0}{2} + a_1 \cos t + a_2 \cos 2t + \cdots b_1 \sin t + b_2 \sin 2t + \cdots \right) \cos kt
\]となりますね。
さらに両辺を \( - \pi \) から \( \pi \) で定積分しましょう。
すると、
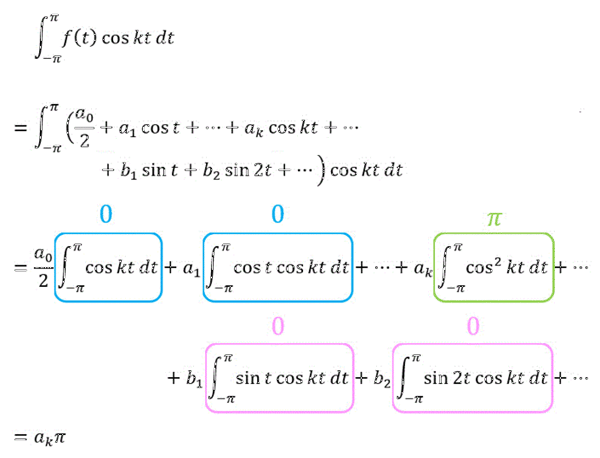
と計算できます。
よって、\[
\int^{\pi}_{- \pi} f(t) \cos kt \ dt = a_k \pi
\]より、\[
a_k = \frac{1}{\pi} \int^{\pi}_{- \pi} f(t) \cos kt \ dt
\]と導出できます。
ここで初項 \( a_0 / 2 \) の \( 2 \) の意味を考えてみましょう。
\[\begin{align*}
a_0 &
= \frac{1}{\pi} \int^{\pi}_{- \pi} f(t) \ dt
\\ &
= \frac{1}{\pi} \int^{\pi}_{- \pi} f(t) \cos 0 \ dt
\end{align*}\]
初項の場合は \( k = 0 \) なので、\( a_0 \) を \( a_k \) と同じ形で表現することができますね!
初項をあえて \( a_0 / 2 \) にしているのは \( a_0 \) を \( a_k \) と同じ形にするためだったのです!*5
(覚えるべき公式も減りますし!)
(iii) sin の項の導出 \( b_k \)
最後に奇関数 \( \sin kx \) のフーリエ係数 \( b_k \) を導出してみましょう。
\[
f(t) = \frac{a_0}{2} + a_1 \cos t + a_2 \cos 2t + \cdots b_1 \sin t + b_2 \sin 2t + \cdots
\]の両辺に \( \sin kt \) を掛けましょう。
すると、\[
f(t) \sin kt = \left( \frac{a_0}{2} + a_1 \cos t + a_2 \cos 2t + \cdots b_1 \sin t + b_2 \sin 2t + \cdots \right) \sin kt
\]となりますね。
さらに両辺を \( - \pi \) から \( \pi \) で定積分しましょう。
すると、
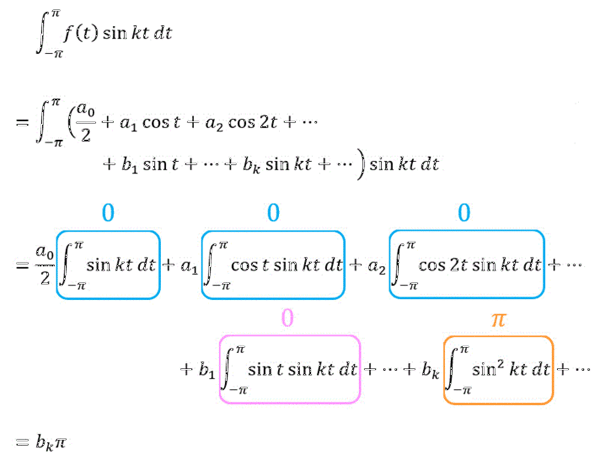
となりますね!
<
よって、\[
\int^{\pi}_{- \pi} f(t) \sin kt \ dt = b_k \pi
\]より、\[
b_k = \frac{1}{\pi} \int^{\pi}_{- \pi} f(t) \sin kt \ dt
\]と導出できます。
ところで \( \cos \) の初項 \( a_0 \) はあったのになぜ \( \sin \)の初項 \( b_0 \) がないのかと思った人もいるかもしれません。
先ほどの公式に \( b = 0 \) を入れてみると、\[
b_0 = \frac{1}{\pi} \int^{\pi}_{- \pi} f(t) \sin 0 \ dt = 0
\]となり、\( \sin 0 \) のおかげで0になってしまいます。
なので、奇関数の初項 \( b_0 \) は計算する必要がないのです!
(2) f(t)が偶関数・奇関数の場合
周期関数 \( f(t) \) が偶関数・奇関数の場合はより少ない計算量でフーリエ級数展開を求めることができます。
(i) f(t) が偶関数の場合
\( f(t) \) が偶関数の場合、\( f(t) \) と \( \sin kt \) の積 \( f(t) \sin kt \)は奇関数となりますね。
なので、\[
b_k = \frac{1}{\pi} \int^{\pi}_{- \pi} f(t) \sin kt \ dt = 0
\]となります。
(ii) f(t) が奇関数の場合
\( f(t) \) が奇関数の場合、\( f(t) \) と \( \cos kt \) の積 \( f(t) \cos kt \)は奇関数となりますね。
なので、\[
a_k = \frac{1}{\pi} \int^{\pi}_{- \pi} f(t) \cos kt \ dt = 0
\]となります。
(もちろん \( a_0 = 0 \) です。
)
周期 \( 2 \pi \) の周期関数 \( f(t) \) が偶関数のとき、\( b_k = 0 \) となる。
なので、フーリエ級数展開は\[
f(t) \approx \frac{a_0}{2} + \sum^{\infty}_{k = 1} a_k \cos k t \]となる。
(フーリエ余弦級数、フーリエ・コサイン級数と呼ばれます。)
また、周期関数 \( f(t) \) が奇関数のとき、\( a_0 = 0 \), \( a_k = 0 \) となる。
なのでフーリエ級数展開は、\[
f(t) \approx \sum^{\infty}_{k = 1} b_k \sin k t
\]となる。
(フーリエ正弦級数、フーリエ・サイン級数と呼ばれます。)
周期2πの偶関数・奇関数のときのフーリエ級数展開
4.周期Tの場合のフーリエ級数展開の公式
先ほどは周期が \( 2 \pi \) の場合に固定したフーリエ級数展開の公式についてまとめました。
ですが、実際の周期関数(波形とか)が \( 2 \pi \) に固定されてるなんてそんな都合のいいことはありませんね。
例えば安静時の心電図の波形の周期は約1秒弱*6ですし、コンセントから供給される電源は50kHzか60kHzなので17〜20μ秒周期ですね。
なので今度はあらゆる周期に対応したフーリエ級数展開の公式を考えてみましょう。
周期 \( 2\pi \) だったものが周期 \( T \) に変化すると、単位時間あたりに進む波の速さは、\[
\frac{2 \pi}{T}
\]倍となります。
ここで、物理をやったことがある人なら「見たことあるような式」だなと思ったかもしれません。
実はこれ、角速度*7 \( \omega \) を求める式と全く同じなのです! なので、\[
\omega = \frac{2 \pi}{T}
\]としてあげましょう。
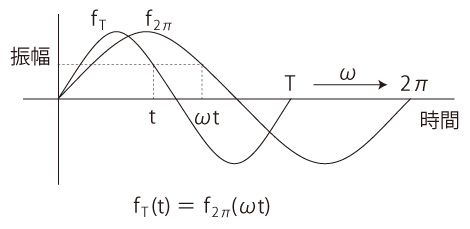
すると、周期 \( 2\pi \) だった場合のフーリエ級数の式
\[
f(t) \approx \frac{a_0}{2} + \sum^{\infty}_{k = 1} \left( a_k \cos k t + b_k \sin k t \right)
\]
の \( t \) が \( \omega t \)(\( \omega \) 倍)となり、周期 \( T \) の場合のフーリエ級数展開の式は
\[
f(t) \approx \frac{a_0}{2} + \sum^{\infty}_{k = 1} \left( a_k \cos k \omega t + b_k \sin k \omega t \right)
\]
と書き換えられます。
\[
\quad ∵ f_T(t) = f_{2 \pi}(\omega t) \approx \frac{a_0}{2} + \sum^{\infty}_{k = 1} \left( a_k \cos k \omega t + b_k \sin k \omega t \right)
\]
\( t \) が \( \omega t \) となったので \( a_k \), \( b_k \) の値も当然変わりますね。
それぞれ計算していきましょう。
まず周期 \( 2 \pi \) の場合の \( a_k \), \( b_k \) の積分範囲を \( - \pi \to \pi \) から \( 0 \to 2\pi \) と書き換えます*8。
\( t = \omega s \) とおくと、\( a_k \), \( b_k \) の積分範囲、\( dt \) と [ds] の関係式は\[
dt = \omega \ ds = \frac{2 \pi}{T} \ ds , \ \ \ 0 \to T
\]となりますね。
よって、積分式は、\[
a_k = \frac{1}{\pi} \int^{2 \pi}_{0} f(t) \cos kt \ dt = \frac{2}{T} \int^{ T }_{ 0 } \cos k \omega s \ ds
\\
b_k = \frac{1}{\pi} \int^{2 \pi}_{0} f(t) \sin kt \ dt = \frac{2}{T} \int^{ T }_{ 0 } \sin k \omega s \ ds
\]と変化します。
あとは変数 \( s \) を \( t \) に戻すことで\[
a_k = \frac{2}{T} \int^{ T }_{ 0 } \cos k \omega t \ dt \\
b_k = \frac{2}{T} \int^{ T }_{ 0 } \sin k \omega t \ dt
\]となります。
周期Tのフーリエ級数展開の公式
周期 \( T \) の区分的に連続な周期関数 \( f(t) \) のとき、\[
f(t) \approx \frac{a_0}{2} + \sum^{\infty}_{k = 1} \left( a_k \cos k \omega t + b_k \sin k \omega t \right)
\]と表せる。
ただし、\[
a_k = \frac{2}{T} \int^{T}_{0} f(t) \cos k \omega t \ dt \ \ (k = 0,1,2,3, \cdots) \\
b_k = \frac{2}{T} \int^{T}_{0} f(t) \sin k \omega t \ dt \ \ (k = 1,2,3, \cdots)
\]となる。
※積分範囲は \( 0 \) から \( T \) ではなく、例えば \( -T/2 \) から \( T/2 \) としてもよい。
とにかく1周期分積分していればどこでもよい。
こちらも色などをつけてみやすく表現したバージョンも用意しました。

周期が \( 2 \pi \) から \( T \) になっても周期関数が \( f(t) \) が偶関数・奇関数の場合は計算を楽にすることができます。
周期 \( T \) の周期関数 \( f(t) \) が偶関数のとき、\( b_k = 0 \) となる。
なので、フーリエ級数展開は\[
f(t) \approx \frac{a_0}{2} + \sum^{\infty}_{k = 1} a_k \cos k \omega t \]となる。
(フーリエ余弦級数、フーリエ・コサイン級数と呼ばれます。
)
また、周期関数 \( f(t) \) が奇関数のとき、\( a_0 = 0 \), \( a_k = 0 \) となる。
なのでフーリエ級数展開は、\[
f(t) \approx \sum^{\infty}_{k = 1} b_k \sin k \omega t
\]となる。
(フーリエ正弦級数、フーリエ・サイン級数と呼ばれます。
)
周期Tの偶関数・奇関数のときのフーリエ級数展開
ではここで1問計算練習をしてみましょう!
例題
下の図ような周期関数\[
f(t) = t( \pi - t) = -t^2 + t \pi
\]を考える。
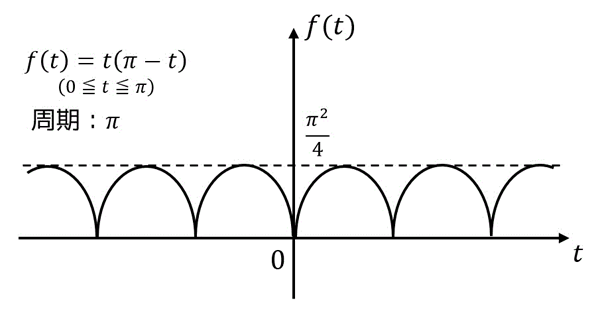
\( f(t) \) のフーリエ級数展開を求めなさい。
解説
\( f(t) \) は連続関数なので、\[
f(t) \approx \frac{a_0}{2} + \sum^{\infty}_{k = 1} \left( a_k \cos k \omega t + b_k \sin k \omega t \right)
\]とフーリエ級数展開できる。
また、周期が \( \pi \) なので角速度 \( \omega \) は、\[
\omega = \frac{ 2 \pi}{\pi} = 2
\]となる。
さらにグラフより \( f(-t) = f(t) \) が成り立つので \( f(t) \) は偶関数である。
よって \( b_k = 0 \) となり、\[
f(t) \approx \frac{a_0}{2} + \sum^{\infty}_{k = 1} a_k \cos 2k t
\]となる。
(i) \( k = 0 \)、つまり \( a_0 \) のとき
\[ \begin{align*}
a_0 & = \frac{2}{T} \int^{\pi}_{0} (-t^2 + t \pi ) \cos 0 \ dt
\\ & = \frac{2}{\pi} \int^{\pi}_{0} -t^2 + t \pi \ dt
\\ & = \frac{2}{\pi} \left[ - \frac{1}{3} t^3 + \frac{1}{2} t^2 \pi \right]^{\pi}_{0}
\\ & =\frac{2}{\pi} \left( - \frac{1}{3} \pi^3 + \frac{1}{2} \right)
\\ & = \frac{2}{\pi} \cdot \frac{1}{6} \pi^3
\\ & = \frac{1}{3} \pi^2
\end{align*} \]
(ii) \( k \geqq 1 \)、つまり \( a_k \) のとき
多項式と三角関数の積で表された関数を積分する際には部分積分を行うのですが、部分積分の連鎖公式を適用していくと比較的早く部分積分を行うことができます。
計算式は、\[ \begin{align*}
a_k & = \frac{2}{\pi} \int^{\pi}_{0} (-t^2 + t \pi) \cos 2kt \ dt
\\ & = \frac{2}{\pi} \left[ \frac{1}{2k} (- t^2 + t \pi) \sin 2kt - \left( - \frac{1}{4k^2} (- 2t + \pi) \cos 2kt \right) + \left( - \frac{1}{8k^3} (-2) \cdot \sin 2kt \right) \right]^{\pi}_{0}
\\ & = \frac{2}{\pi} \left[ \frac{1}{4k^2} (- 2t + \pi) \cos 2kt \right]^{\pi}_{0}
\\ & = \frac{2}{\pi} \left( \frac{1}{4k^2} ( - \pi - \pi ) \right)
\\ & = - \frac{1}{k^2}
\end{align*}\]となる。
よって、\[
f(t) \approx \frac{1}{6} \pi^2 - \sum^{\infty}_{k = 1} \frac{1}{k^2} \cos 2k t
\]となる。
5.フーリエ級数展開を用いた無限級数の求め方
先ほど求めたフーリエ級数展開から様々な無限級数の和を導くことができます。
先ほど求めた周期が \( \pi \) の周期関数\[
f(t) = t( \pi - t) = -t^2 + t \pi
\]に \( t = 0 \) を代入すると、\[\begin{align*}
f(0) & = \frac{1}{6} \pi^2 - \sum^{\infty}_{k = 1} \frac{1}{k^2} \cos 0
\\ & = \frac{1}{6} \pi^2 - \sum^{\infty}_{k = 1} \frac{1}{k^2} = 0
\end{align*}\]が成立しますよね。
よって、\[\begin{align*}
\sum^{\infty}_{k = 1} \frac{1}{k^2} & = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots
\\ & = \frac{\pi^2}{6}
\end{align*}\]を示すことができます。
(この無限級数はバーゼル問題と呼ばれています。
)
さらに \( t = \pi/2 \) を代入すると、\[\begin{align*}
f( \frac{\pi}{2} ) & = \frac{1}{6} \pi^2 - \sum^{\infty}_{k = 1} \frac{1}{k^2} \cos k \pi
\\ & = \frac{1}{6} \pi^2 - \sum^{\infty}_{k = 1} \frac{1}{k^2} (-1)^k = \frac{\pi^2}{4}
\end{align*}\]が成立しますよね。
よって、\[\begin{align*}
- \sum^{\infty}_{k = 1} \frac{1}{k^2} (-1)^k & = \frac{1}{1^2} - \frac{1}{2^2} + \frac{1}{3^2} - \frac{1}{4^2} + \cdots
\\ & = \frac{\pi^2}{4} - \frac{\pi^2}{6}
\\ & = \frac{\pi^2}{12}
\end{align*}\]となり、無限級数\[
\frac{1}{1^2} - \frac{1}{2^2} + \frac{1}{3^2} - \frac{1}{4^2} + \cdots = \frac{\pi^2}{12}
\]を示すことができます!
ただし、このようにフーリエ級数展開から無限級数を求める際には、代入する \( t \) の値において必ず連続である(グラフが途切れていない)ことが条件となります。
6.練習問題
では、3問ほど練習してみましょう!
練習1
下の図のような周期関数\[
f(t) = |t|
\]を考える。
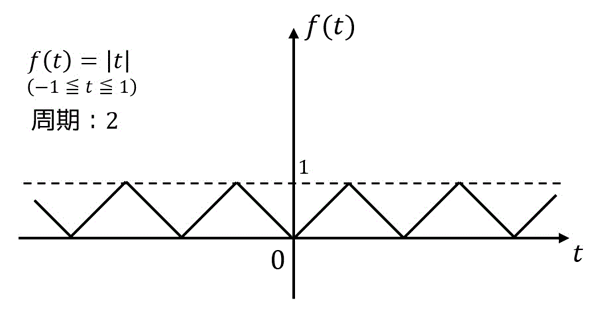
(1) \( f(t) \) のフーリエ級数展開を求めなさい。
(2) (1)から\[
\frac{1}{1^2} + \frac{1}{3^2} + \frac{1}{5^2} + \cdots
\]の値を求めなさい。
練習2
下の図のような周期関数\[
f(t) = |\sin t \ |
\]を考える。
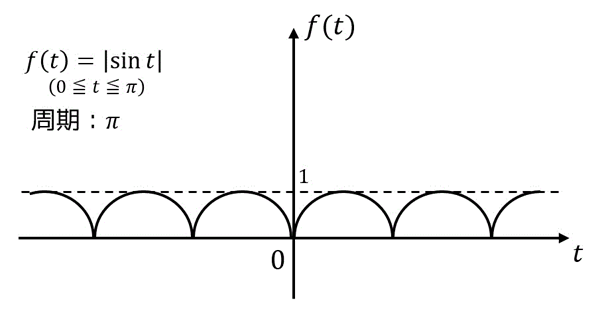
(1) \( f(t) \) のフーリエ級数展開を求めなさい。
(2) (1)から\[
\frac{1}{1 \cdot 3} - \frac{1}{3 \cdot 5} + \frac{1}{5 \cdot 7} - \frac{1}{7 \cdot 9} + \cdots
\]の値を求めなさい。
練習3
下の図のような周期関数\[
f(t) = 1 - \frac{t}{\pi}
\]を考える。
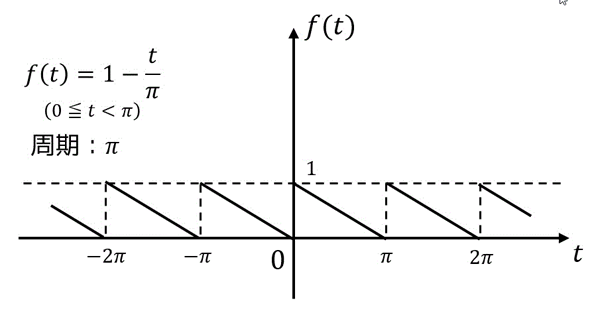
(1) \( f(t) \) のフーリエ級数展開を求めなさい。
[ヒント] \( g(t) \) を\[
g(t) = f(t) - \frac{1}{2}
\]とおく。
(2) (1)から\[
\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} \cdots
\]の値を求めなさい。
7.練習問題の答え
解答1
(1)
\( f(-t) = f(t) \) が成立するので、\( f(t) \) は偶関数である。
また、周期 \( T \) は2なので、角速度 \( \omega \) は\[
\frac{2 \pi}{2} = \pi
\]となる。
よって、\[
f(t) \approx \frac{a_0}{2} + \sum^{\infty}_{k = 1} a_k \cos k \pi t
\]とフーリエ級数展開できる。
(i) \( k = 0 \)、つまり \( a_0 \) のとき
\[ \begin{align*}
a_0 & = \frac{2}{2} \int^{1}_{-1} |t| \cos 0 \ dt
\\ & = 2 \int^{1}_{0} t \ dt
\\ & = 2 \left[ \frac{1}{2} t^2 \right]^{1}_{0}
\\ & = 2 \cdot \frac{1}{2}
\\ & = 1
\end{align*} \]となる。
(ii) \( k \geqq 1 \)、つまり \( a_k \) のとき
\[ \begin{align*}
a_k & = \frac{2}{2} \int^{1}_{-1} |t| \cos k \pi t \ dt
\\ & = 2 \int^{1}_{0} t \cos k \pi t \ dt
\\ & = 2 \left[ \frac{1}{k \pi} \sin k \pi t - \left( - \frac{1}{k^2 \pi^2} \cos k \pi t \right) \right]^{1}_{0}
\\ & = 2 \cdot \frac{1}{k^2 \pi^2} \cdot \left( \cos k \pi - 1 \right)
\\ & = \frac{2}{k^2 \pi^2} \left( (-1)^k - 1 \right)
\end{align*} \]となる。
よって、フーリエ級数展開は\[
f(t) \approx \frac{1}{2} + \sum^{\infty}_{k = 1} \frac{2}{k^2 \pi^2} \left( (-1)^k - 1 \right) \cos k \pi t
\]と求められる。
(2)
\( f(t) \) は \( t = 0 \) において連続なので \( f(t) \) とフーリエ級数展開の値が \( t = 0 \) において一致する。
よって、\( t = 0 \) を代入すると、\[\begin{align*}
f(0) & = \frac{1}{2} + \sum^{\infty}_{k = 1} \frac{2}{k^2 \pi^2} \left( (-1)^k - 1 \right) \cos 0
\\ & = \frac{1}{2} + \frac{2}{\pi^2} \sum^{\infty}_{k = 1} \left( (-1)^k - 1 \right)
\\ & = 0
\end{align*}\]となる。
ここで、\[
- \frac{2}{\pi^2} \sum^{\infty}_{k = 1} \left( (-1)^k - 1 \right) = \frac{1}{2}
\]が成立する。
目標の形は、\[\begin{align*}
- \frac{1}{2} \sum^{\infty}_{k = 1} \left( (-1)^k - 1 \right) = \frac{1}{1^2} +\frac{1}{3^2} + \frac{1}{5^2} + \cdots
\end{align*}\]なので、上で導出した式に \( \pi^2 / 4 \) 倍すればよい*9。
よって、\[\begin{align*}
- \frac{1}{2} \sum^{\infty}_{k = 1} \left( (-1)^k - 1 \right) & = \frac{1}{1^2} +\frac{1}{3^2} + \frac{1}{5^2} + \cdots
\\ & = \frac{1}{2} \cdot \frac{ \pi} {4} = \frac{\pi^2}{8}
\end{align*}\]となる。
解答2
(1)
\( f(-t) = f(t) \) が成立するので、\( f(t) \) は偶関数である。
また、\( f(t) \) の周期 \( T \) は \( \pi \) なので、角速度 \( \omega \) は\[
\frac{2 \pi}{\pi} = 2
\]となる。
よって、\[
f(t) \approx \frac{a_0}{2} + \sum^{\infty}_{k = 1} a_k \cos 2k t
\]とフーリエ級数展開できる。
(i) \( k = 0 \)、つまり \( a_0 \) のとき
\( 0 \leqq t \leqq 1 \) において \( \sin t \geqq 0 \) なので、\( | \sin t \ | = \sin t \) である。
よって、\[ \begin{align*}
a_0 & = \frac{2}{\pi} \int^{\pi}_{0} \sin t \ dt
\\ & = \frac{2}{\pi} \left[ - \cos t \right]^{\pi}_{0}
\\ & = \frac{2}{\pi} (1 + 1)
\\ & = \frac{4}{\pi}
\end{align*} \]となる。
(ii) \( k \geqq 1 \)、つまり \( a_k \) のとき
\( 0 \leqq t \leqq 1 \) において \( \sin t \geqq 0 \) なので、\( | \sin t \ | = \sin t \) である。
よって、\[ \begin{align*}
a_k & = \frac{2}{\pi} \int^{\pi}_{0} \sin t \cos 2nt \ dt
\\ & = \frac{1}{\pi} \int^{\pi}_{0} \sin (1-2n)t \ dt + \frac{1}{\pi} \int^{\pi}_{0} \sin (1+2n)t \ dt
\\ & = \frac{1}{\pi} \left[ \frac{-1}{1-2n} \cos (1-2n) t \right]^{\pi}_{0} + \frac{1}{\pi} \left[ \frac{-1}{1+2n} \cos (1+2n) t \right]^{\pi}_{0}
\\ & = \frac{2}{\pi} \left( \frac{1}{1+2n} - \frac{1}{1 - 2n } \right)
\\ & = \frac{4}{\pi} \cdot \frac{1}{1-4n^2}
\\ & = \frac{4}{\pi} \cdot \frac{1}{(1-2n)(1+2n)}
\\ & = - \frac{4}{\pi} \cdot \frac{1}{(2n-1)(2n+1)}
\end{align*} \]となる。
よって、フーリエ級数展開は\[
f(t) \approx \frac{2}{\pi} - \sum^{\infty}_{k = 1} \frac{4}{\pi} \cdot \frac{1}{(2n-1)(2n+1)} \cos 2k t
\]と求められる。
(2)
\( f(t) \) は \( t = \pi / 2 \) において連続なので \( f(t) \) とフーリエ級数展開の値が \( t = 0 \) において一致する。
よって、\( t = \pi / 2 \) を代入すると、\[\begin{align*}
f( \frac{\pi}{2} ) & = \frac{2}{\pi} - \sum^{\infty}_{k = 1} \frac{4}{\pi} \cdot \frac{1}{(2n-1)(2n+1)} \cos 2k t
\\ & = \frac{2}{\pi} - \frac{4}{\pi} \sum^{\infty}_{k = 1} \cdot \frac{1}{(2n-1)(2n+1)} \cos k \pi
\\ & = 1
\end{align*}\]となる。
よって、\[\begin{align*}
\frac{4}{\pi} \sum^{\infty}_{k = 1} \frac{1}{(2n-1)(2n+1)} \cos k \pi = 1 - \frac{2}{\pi}
\end{align*} \]
目標の形は、\[\begin{align*}
\sum^{\infty}_{k = 1} \frac{1}{(2n-1)(2n+1)} \cos k \pi = \frac{1}{1 \cdot 3} + \frac{1}{3 \cdot 5} + \frac{1}{5 \cdot 7} + \cdots
\end{align*}\]なので、上で導出した式に \( \pi / 4 \) 倍すればよい。
よって、\[\begin{align*}
\sum^{\infty}_{k = 1} \frac{1}{(2n-1)(2n+1)} \cos k \pi & = \frac{1}{1 \cdot 3} + \frac{1}{3 \cdot 5} + \frac{1}{5 \cdot 7} + \cdots
\\ & = \frac{\pi}{4} - \frac{1}{2}
\end{align*}\]となる。
解答3
\( g(t) \) を\[
g(t) = f(t) - \frac{1}{2} = \frac{1}{2} - \frac{t}{\pi}
\]とする。
すると、グラフは
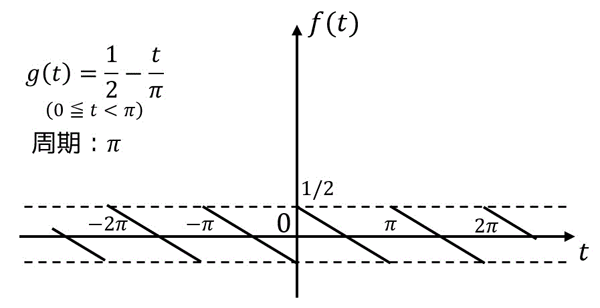
となる。
グラフより、\( g(-t) = - g(t) \) が成立するので \( g(t) \) は奇関数となる。
さらに周期 \( T \) は \( \pi \) なので角速度 \( \omega \) は\[
\frac{2 \pi}{\pi} = 2
\]となる。
よって、\[
g(t) \approx \sum^{\infty}_{k = 1} b_k \sin 2k t
\]とフーリエ級数展開できる。
\( b_k \) の値は、\[\begin{align*}
b_k & = \frac{2}{\pi} \int^{\pi}_{0} f(t) \left( \frac{1}{2} - \frac{t}{\pi} \right) \sin 2k t \ dt
\\ & = \frac{2}{\pi} \left[ - \frac{1}{2k} \left( \frac{1}{2} - \frac{t}{\pi} \right) \cos 2k t - \left( - \frac{1}{2k} \right) \left( - \frac{1}{4k^2} \cdot \left( - \frac{1}{\pi} \right) \right) \sin 2k t \right]^{\pi}_{0}
\\ & = \frac{2}{\pi} \left[ - \frac{1}{2k} \left( \frac{1}{2} - \frac{t}{\pi} \right) \cos 2k t\right]^{\pi}_{0}
\\ & = \frac{2}{\pi} \left( - \frac{1}{2k} \cdot \left( - \frac{1}{2} \right) - \frac{-1}{2k} \cdot \frac{1}{2} \right)
\\ & = \frac{2}{\pi} \cdot \frac{1}{2k}
\\ & = \frac{1}{k \pi}
\end{align*}\]となる。
よって、フーリエ級数展開は\[\begin{align*}
f(t) & = g(t) + \frac{1}{2}
\\ & \approx \frac{1}{2} + \sum^{\infty}_{k = 1} \frac{1}{k \pi} \sin 2k t
\end{align*}\]と求められる。
(2)
\( f(t) \) は \( t = \pi / 4 \) において連続なので \( f(t) \) とフーリエ級数展開の値が \( t = \pi / 4 \) において一致する。
よって、\( t = pi / 4 \) を代入すると\[\begin{align*}
f( \frac{\pi}{4} ) & = \frac{1}{2} + \sum^{\infty}_{k = 1} \frac{1}{k \pi} \sin \frac{\pi}{2} k
\\ & = \frac{1}{2} + \frac{1}{\pi} \sum^{\infty}_{k = 1} \frac{1}{k} \sin \frac{\pi}{2} k \pi
\\ & = \frac{3}{4}
\end{align*}\]となる。
よって、\[\begin{align*}
\frac{1}{\pi} \sum^{\infty}_{k = 1} \frac{1}{k} \sin \frac{\pi}{2} k \pi & = \frac{3}{4} - \frac{1}{2}
\\ & = \frac{1}{4}
\end{align*} \]が成立する。
目標の形は、\[\begin{align*}
\sum^{\infty}_{k = 1} \frac{1}{k} \sin \frac{\pi}{2} k \pi = \frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots
\end{align*}\]なので、上で導出した式に \( \pi \) 倍すればよい。
よって、\[\begin{align*}
\sum^{\infty}_{k = 1} \frac{1}{k} \sin \frac{\pi}{2} k \pi & = \frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots
\\ & = \frac{\pi}{4}
\end{align*}\]となる。
8.さいごに
今回はフーリエ級数展開の簡単なしくみ、および計算方法を例題などを踏まえながらまとめました。
この記事を読んでフーリエ級数展開の仕組みなどが少しでもわかっていただければ本当にありがたいです。
余裕があれば複素フーリエ級数展開、フーリエ変換についてもまとめてみようかと思います。
また、フーリエ級数展開の計算は結構めんどくさいものが多いのでしっかりと計算練習をしておきましょう。