- 今日数学では,「関数」を (集合論において) つぎのように定義します:
| (*) |
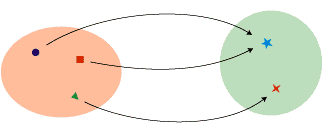
「一方の世界 (集合) の各メンバー (要素) に
他方の世界 (集合) のメンバー (要素) が一つ,しかもただ一つ対応する」
|
言い回し(*) には,つぎの意味が含まれていることに,注意して下さい:
- 左の集合のどの要素からも矢線がのびて右の集合のどれかの要素に届きます。
- 右の集合には矢線が届いてこない要素があるかも知れません。
- 一つの要素から2本以上の矢線が発することはありません。
- 「一方の要素に他方の要素が一つ,しかもただ一つ対応する」ことを,「一意対応」と呼びます。(「一意 (unique)」の意味は「相手が一通りに決まる」)
「一意対応」を関数の条件とするのは,つぎのことを意識しているからです:
- 「ものが同じならば,値も同じ」
- 「入力が同じならば,出力も同じ」
- 「原因が同じならば,結果も同じ」
- 上の図の左側の集合と右側の集合の呼び名ですが,集合論的な関数論では,「始集合・終集合」や「domain・codomain」が使われます。
伝統的な呼び名は「定義域 (domain)・値域 (range)」ですが,これは「関数」の意味が「一意対応」ではない時代のものですので,「始集合・終集合」とは意味がずれてきます。
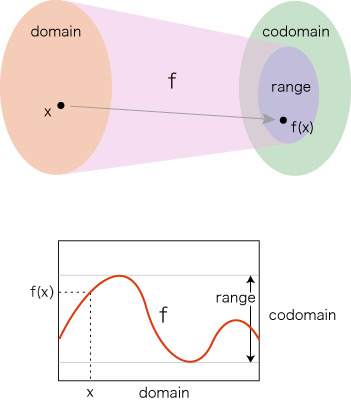
実際,関数の像 (image) のことを「値域」と呼んで,「domain・range・codomain」の用語セットをつくる立場があります:
|



